1 - Einführung - Prof. Dr. Matthias Rarey - Universität Hamburg
Videokatalog

Video-Player wird geladen.
Aktueller Zeitpunkt 0:00
/
Dauer 1:30:14
Geladen: 0.11%
0:00:00
Streamtyp LIVE
Verbleibende Zeit -1:30:14
1x
- 1.5x
- 1.25x
- 1x, ausgewählt
- 0.75x
- Beschreibungen aus, ausgewählt
- Untertiteleinstellungen, öffnet Einstellungen für Untertitel
- Untertitel aus, ausgewählt
- Deutsch (automatisch erzeugt) Untertitel
- default, ausgewählt
This is a modal window.
Anfang des Dialogfensters. Esc bricht ab und schließt das Fenster.
Ende des Dialogfensters.
6317 Aufrufe
Technischer Support
Bitte klicken Sie auf den nachfolgenden Link und füllen Sie daraufhin die notwendigen Felder aus, um unser Support-Team zu kontaktieren!
Link zu der RRZ-Support-Seite
Untertitel
00:00:01
So, einen wunderschönen guten Morgen. Ich weiß nicht,
00:00:05
wie Akustik in diesen heiligen Hallen sind.
00:00:08
Können Sie mich verstehen da hinten? Hervorragend. Gut.
00:00:14
Ja, willkommen zur Vorlesung Algorithmik. Es freut mich,
00:00:18
so viele hier zu sehen. Ich habe die Vorlesung 2007,
00:00:24
das erste Mal hier in Hamburg angeboten. Zu dem Zeitpunkt
00:00:28
gab es so ähnliches auf Masterlevel noch nicht hier in Hamburg.
00:00:34
Und damals hatten wir hier so mit vier,
00:00:35
fünf Leuten gesessen. Und deswegen freut mich das natürlich,
00:00:39
dass das so ein großes Interesse,
00:00:40
dass sie ein großes Interesse da ist an der Veranstaltung
00:00:43
Ich hoffe, dass sie mir auch alle erhalten bleiben.
00:00:48
Und über die Zeit. So, okay, was machen wir? Ja,
00:00:55
heute erzähle ich Ihnen die ersten fünf Minuten ein bisschen was Organisatorisches.
00:00:59
Und dann legen wir auch gleich los. Ich weiß nicht,
00:01:04
ja, Sie können aus verschiedenen Gründen zunächst einmal hier sein.
00:01:08
Wie viele Bachelor haben wir hier? Wer ist Bachelor?
00:01:12
Okay, eine Handvoll. Und Rest des Master nehme ich
00:01:16
mal an.
00:01:17
Wer ist nicht Master-Informatik
00:01:21
Das sind die Bioinformatiker, die ich alle kenne.
00:01:25
Und was Diplom. Okay, okay. Gibt es noch
00:01:29
irgendeinen Wahl-Nebenfachstudierenden, Mathematiker, Physiker? Okay. Prima.
00:01:39
Okay, gut. So, also Vorlesungen. Das wissen
00:01:43
Sie, sonst säßen Sie nicht hier. Der Grund,
00:01:46
warum ich hier nochmal hinschreibe, ist,
00:01:49
weil ich immer am Anfang nochmal bespreche, gibt es irgendeinen Grund,
00:01:53
das zeitlich noch so ein bisschen zu verschieben,
00:01:55
so 15-Minuten-Spiel haben wir ja.
00:01:59
Müssen Sie irgendwo hin? Sollen wir
00:02:01
um 10 Uhr anfangen
00:02:05
10 anfangen, können wir länger mit lauten Bocken machen.
00:02:08
Vorsichtig, das ist eine gute Idee. Also mir wäre das in beiden Tagen,
00:02:13
egal ob wir um 10 Uhr oder um 10.15 Uhr anfangen,
00:02:15
also können wir auch abstimmen. Also wer ist für 10 Uhr?
00:02:22
Oha, jetzt ist es schwierig. 1, 2,
00:02:25
3, 4, 5, 6, 7,
00:02:28
8, 9. Ich glaube, das sieht schlecht aus.
00:02:32
Die Langschläfer haben gewonnen. Also bleibt es bei 10.15 Uhr. Gut,
00:02:40
wenn Sie mich sprechen möchten, können Sie das Ja,
00:02:46
jederzeit tun, entweder nach der Vorlesung,
00:02:48
können Sie zu mir kommen, wenn Sie ein kurzes Anliegen haben,
00:02:51
wenn Sie ein bisschen länger mit mir sprechen möchten, können Sie am besten ins Set BH.
00:02:57
Wir sitzen in der Bundesstraße 43, also ich habe hier auf dem Campus keine Büros. Das ist also ein Gebäude,
00:03:04
zwei neben dem Geomatikum an der Bundesstraße und ich habe keine festen Termine,
00:03:11
wenn Sie mit mir sprechen wollen,
00:03:13
schicken Sie einfach eine E-Mail an die Melanie Geringhoff und sagen Sie ja schon,
00:03:17
wann es Ihnen gut passt,
00:03:19
weil vielleicht haben Sie dann einen Zeitpunkt,
00:03:19
wo Sie sowieso mal auf dem Hauptcampus sind und dann sagen Sie dann und dann vielleicht und dann versucht Sie das einzurichten,
00:03:26
melden Sie sich einfach,
00:03:27
wenn Sie
00:03:27
mit mir sprechen möchten
00:03:30
Okay, so, zur Übung. Es gibt drei Übungstermine.
00:03:35
Ich hoffe, Sie sind alle in irgendeiner dieser drei Übungsgruppen gelandet.
00:03:40
Die eine ist Montag, die anderen beiden sind am Mittwoch parallel.
00:03:47
Das sind die Übungsgruppenleiter, das sind Doktoranden aus meiner Arbeitsgruppe,
00:03:51
das ist der Thomas Otto, Florian Laug und Tirese Inester.
00:03:56
Und die können Sie alle auch per E-Mail erreichen,
00:04:00
wenn Sie das mal müssen. Das sehen Sie hier.
00:04:05
Und ansonsten sitzen die auch alle im ZBH,
00:04:07
das heißt alle auch nicht hier,
00:04:08
sondern in der Bundesstraße
00:04:12
Gut, der Übungsbetrieb wird so ablaufen, dass wir Übungszettel verteilen.
00:04:18
Das machen wir über Stine. Das heißt,
00:04:22
sie müssen sich unter Stine mal einmal einloggen und wir werden
00:04:26
das immer am Montag, im Laufe des Tages machen.
00:04:30
Also wir versuchen das immer schon bis Montagmittag spätestens,
00:04:33
aber manchmal ist es dann so,
00:04:34
dass wir noch an der einen oder anderen Stelle ein bisschen feilen und
00:04:37
damit sie nicht dann um Punkt 12 gucken und sagen,
00:04:39
ist ja gar nicht da.
00:04:40
Also irgendwann im Laufe des Montags bekommen sie einen Übungszettel und
00:04:45
der ist dann unter Stine unter der Vorlesung
00:04:49
Finden. Dann haben sie sieben Tage Zeit,
00:04:51
den zu bearbeiten und weil ich den Abgabezeitpunkt dann nicht so flexibel machen wollte wie hier,
00:04:59
habe ich dann gesagt, okay,
00:05:00
dann machen wir einfach den nächsten Tag, also Dienstagmorgen,
00:05:03
das heißt, sie können dann Montag noch den ganzen Tag irgendwie daran arbeiten,
00:05:06
meinetwegen auch die ganze Nacht,
00:05:07
weil Dienstags haben sie ja keine Vorlesung,
00:05:09
da können sie dann auch müde sein.
00:05:12
Und dann geben sie Dienstagmorgen die Vorlesung ab, den Übungszettel ab.
00:05:19
Das geht am einfachsten, wenn sie es elektronisch haben,
00:05:25
per E-Mail an ihren Übungsgruppenleiter
00:05:29
Wenn sie das elektronisch da einreichen, bitte nur PDF und
00:05:34
bitte nur ein Dokument. Das sind die Randbedingungen. Nicht,
00:05:38
dass sie da irgendwie eine E-Mail hinschicken mit 15 eingescannten Seiten.
00:05:43
Sie dürfen das gerne handschriftlich machen und einscannen. Dagegen hatte
00:05:46
überhaupt keiner was. Aber dann packen sie es bitte alles in ein PDF-Dokument.
00:05:50
Dann ist das für die Übungsgruppenleiter ein bisschen einfacher. Wenn sie das Ganze handschriftlich machen,
00:05:58
was okay ist, also wir werden hier eigentlich keine Übung haben,
00:06:02
die man nicht einfach nur auf Bleistift,
00:06:04
mit Bleistift und Papier machen kann, dann können sie entweder,
00:06:08
wenn sie es schon fertig haben,
00:06:10
mir das einfach am Montag geben nach der Vorlesung,
00:06:12
sagen,
00:06:13
hier,
00:06:13
wir haben das schon alles fertig,
00:06:14
geben es an
00:06:16
Oder, naja, wenn sie es im Laufe des Tages
00:06:19
dann machen oder dieses Tag ganz früh morgens,
00:06:21
können sie es auch am ZBH abgeben.
00:06:23
Dann müsste ich da allerdings nochmal gucken,
00:06:25
ob wir da noch einen Kassen hinstellen oder so,
00:06:27
wo sie das abgeben können.
00:06:29
Können wir auch noch machen. Okay,
00:06:31
das ist also dann in der darauf folgenden Woche und dann in
00:06:36
der dann darauf folgenden Woche in den Übungen wird der Zettel dann besprochen.
00:06:41
Ja, dann gehen wir das durch und rechnen dann
00:06:45
die Aufgaben zusammen mit ihnen
00:06:50
Ja, wie soll das laufen? Also sie müssen eine
00:06:52
Studienleistung erbringen, dass sie nachher an der Prüfung teilnehmen können.
00:06:58
Sie sollen die Übungsblätter bearbeiten in Gruppen und zwar bevorzugt mit zwei Personen.
00:07:04
Also sie sollen Teams bilden von zwei Personen.
00:07:09
Da man das natürlich nicht letztendlich fordern können,
00:07:11
sie könnten ja eine ungerade Anzahl von Studierenden sein, gehen auch Dreierteams,
00:07:17
aber wirklich nur in Ausnahmefällen versuchen sie zu zweit zusammenzuarbeiten.
00:07:23
Es ist am effektivsten unserer Erfahrung nach. Also sie bilden Zweiergruppen
00:07:30
Und wenn irgendjemand übrig bleibt, dann darf der auch noch
00:07:32
irgendwo dazu. Und dann haben sie auch eine Dreiergruppe.
00:07:33
Machen Sie bitte keine Eiselabgaben. Das Einzelabgaben sind insofern ungünstig,
00:07:40
weil die Korrektur der Übungsblätter,
00:07:42
also wir gucken die ja alle durch und schreiben ihn auch dran,
00:07:46
wenn was falsch ist.
00:07:46
Das kostet halt sehr viel Zeit. Und wenn sie alle einzeln abgeben würden,
00:07:52
dann wäre das für die Übungsgruppen leider kaum mehr zu schaffen.
00:07:56
Okay, dann geben Sie den Zettel ab und sie sammeln
00:08:00
dann Punkte im Laufe des Semesters.
00:08:05
Und wenn sie dann 50 Prozent der Punkte erreicht haben,
00:08:08
dann haben sie
00:08:08
das erste Kriterium
00:08:10
Und dann gibt es noch ein zweites. Und zwar,
00:08:13
dass sie auf mindestens neun von zwölf Blättern,
00:08:15
also es gibt zwölf Blätter, wir haben eigentlich 14 Wochen,
00:08:17
aber wir haben ja diese zwei Wochen Versatz darin.
00:08:19
Deswegen gibt es insgesamt zwölf Blätter. Also mindestens auf neun
00:08:23
dieser zwölf Blätter sollten sie mindestens 20 Prozent der Punkte haben.
00:08:28
Das heißt, es ist eigentlich nichts anderes als die Regel,
00:08:31
dass sie die Übungsblätter auch abgeben sollten und nicht sagen sollten, naja,
00:08:34
ich brauche ja nur 50 Prozent, war ja nur die Hälfte der Zettel bearbeiten.
00:08:39
Ja? Okay, das ist mir insofern wichtig,
00:08:43
weil sie erfahrungsgemäß den Stoff nur dann richtig vertiefen,
00:08:47
wenn sie auch die Übungen dazu machen.
00:08:51
Und ja, weil natürlich in der Prüfung später
00:08:52
auch das ganze Stoffspektrum drankommen kann
00:08:56
Wäre das natürlich dann ungünstig,
00:08:58
wenn sie in Teilen sozusagen nur die Vorlesung gehört hätten.
00:09:04
So, dann sollten sich natürlich auch engagieren in der Übung.
00:09:09
Hier steht mindestens eine erfolgreiche Präsentation einer Teilübungsaufgabe. Und das machen wir so,
00:09:18
da haben wir auch immer viel überlegt, wie wir das machen.
00:09:20
Das Problem ist nämlich immer so ein bisschen bei den Übungen,
00:09:23
wenn man einfach sagt,
00:09:24
ihr müsst das jetzt alles vorstellen und sie sitzen dann als Studenten da und dann Wollen sie vielleicht nicht,
00:09:31
vielleicht ist die Lösung auch nicht ganz optimal und dann steht einer vorne,
00:09:35
stellt das irgendwie vor,
00:09:36
aber es ist suboptimal und die anderen sitzen und hören zu und wollen es eigentlich verstehen und kriegen eigentlich keine optimale Lösung präsentiert.
00:09:42
Deswegen machen wir das so, dass wir der Übungsgruppenleiter,
00:09:48
der kennt ja ihre Lösung,
00:09:49
der hat die ja korrigiert und der sagt,
00:09:53
welche Lösung sozusagen vorgestellt werden können.
00:09:59
Und dann haben sie das ja in einer kleinen Gruppe
00:10:01
gemacht und dann können sie sozusagen im Zweifelsfall entscheiden,
00:10:06
wer es dann macht
00:10:10
Ja, wir haben uns jetzt darauf festgelegt,
00:10:13
dass wir sagen, eine Präsentation reicht aus und wollen sie
00:10:17
natürlich trotzdem animieren dazu, möglichst häufig was vorzustellen.
00:10:22
Und wir haben uns dann überlegt, wir machen das einfach so,
00:10:24
dass wir ihnen einfach Punkte geben,
00:10:26
wenn sie ein zweites oder ein drittes Mal präsentieren.
00:10:29
Wenn sie zehnmal präsentieren, kriegen sie keine Punkte mehr.
00:10:31
Also nur fürs zweite und dritte Mal kriegen sie sozusagen die Punkte,
00:10:35
die sie für die Aufgabe gekriegt hätten, nochmal obendrauf.
00:10:37
Wenn sie dann sagen, ich muss noch ein bisschen Punkte sammeln,
00:10:41
können sie da ein bisschen was gut machen.
00:10:43
Okay, gut,
00:10:45
das zu den Übungsblättern
00:10:49
Vielleicht noch ein bisschen zu dieser Punktezahl und die sind 50 Prozent.
00:10:54
Also viele haben ja so bei den Prozentsaalen immer so Noten im Kopf.
00:10:57
Die sagen dann, ja, die wissen schon,
00:10:58
95 Prozent ist 1-0 und dann
00:11:02
irgendwie 80 Prozent ist noch eine 2 oder so.
00:11:06
Diese Punkte, die sie auf den Übungsblättern haben,
00:11:08
sollten sie nicht in irgendeiner Art und Weise in Noten umrechnen.
00:11:12
Das macht keinen Sinn. Es geht hier nur darum,
00:11:14
zu sehen, dass sie einfach kontinuierlich mitarbeiten.
00:11:18
Das ist sozusagen Sinn und Zweck der ganzen Sache.
00:11:24
Okay, gut,
00:11:27
das dazu
00:11:31
Und dann können wir so langsam den Übergang zum Inhaltlichen machen.
00:11:36
Haben Sie Fragen zum Übungsbetrieb? Ja. Als Volsesbetrieb
00:11:41
wurde auch die Mittwochsvorlesung aufgezeichnet. Ja, genau.
00:11:44
Die werden beide aufgezeichnet. Entschuldigung? Ja, genau.
00:11:50
Auch Lektor drüber. Gibt es da ein Passwort?
00:11:55
Wenn Sie eins setzen wollten, ja. Okay,
00:11:59
nö, ich glaube nicht, dass das nötig ist.
00:12:01
Nö, also können Sie direkt angucken.
00:12:08
So, was machen wir, wir beschäftigen uns mit Algorithmik?
00:12:10
Das ist ein sehr zentrales Gebiet in der Informatik, weil,
00:12:15
ja, weil wir in der Informatik Probleme lösen wollen, Anwendungsprobleme häufig lösen wollen.
00:12:23
Und das hat immer, hat immer mehrere Komponenten.
00:12:27
Zum einen müssen wir Software schreiben, dafür müssen wir,
00:12:31
ja, das ganze Software-Engineering beherrschen, Programmiersprachen beherrschen etc.
00:12:36
Aber wir brauchen natürlich auch gute Lösungsstrategien. Und häufig ist es dann so,
00:12:41
dass wenn man auf so ein Anwendungsproblem schaut,
00:12:43
dann gibt es irgendwo eine so eine knifflige Komponente.
00:12:46
Irgendwie eine so eine Sache, die nicht so ganz klar ist,
00:12:49
man das Problem anfassen soll und wie man es lösen soll,
00:12:53
um eine gute Lösung zu kriegen.
00:12:54
Das sind in der Regel Optimierungsfragestellungen, die irgendwie immer mal wieder auftauchen.
00:13:00
Und genau mit denen beschäftigen wir uns hier und das Ziel der Veranstaltung ist,
00:13:07
sie dafür zu sensibilisieren, diese Stellen,
00:13:09
also diese Probleme und Fragestellungen zu erkennen,
00:13:13
dass sie einen möglichst großen Baukasten kriegen,
00:13:15
wo sie sagen können, ah, das Problem,
00:13:18
das ist so wie das und das gibt es ja schon in der Informatik und da gibt es einen guten Algorithmus und den kann ich nehmen.
00:13:23
Das ist das Zweite und das Dritte ist,
00:13:26
dass sie in der Lage sind, im Zweifel wenn es was ist,
00:13:30
wo es vielleicht nicht irgendeinen tollen Algorithmus gibt,
00:13:32
auch selber was zu entwerfen, um dieses Problem zu lösen.
00:13:36
Das sind sozusagen die Ziele. Das möchte ich gerne erreichen.
00:13:40
Und bei der Algorithmik ist das wie bei vielen Dingen,
00:13:44
das ist ein Learning by doing.
00:13:46
Deswegen schauen wir uns in dieser Vorlesung unheimlich viele Algorithmen an.
00:13:49
Wir schauen uns Probleme an. Wir schauen uns an,
00:13:52
wie diese Probleme gelöst werden, wie die Algorithmen aussehen und
00:13:55
wie die Analysen dazu aussehen.
00:13:57
Das heißt, wie man dann sieht,
00:13:58
dass der Algorithmus A korrekt ist und B eine spezielle Laufzeitschranke einhält.
00:14:02
Und je mehr man davon gesehen hat,
00:14:04
umso mehr lernt man auch,
00:14:07
selber solche Dinge durchzuführen,
00:14:08
also neue Algorithmen halt zu entwerfen
00:14:12
Ja, es gibt eine riesige Menge an Literatur zu diesem ganzen Themenkomplex,
00:14:18
weil er eben so zentral ist in der Informatik.
00:14:21
Ich gehe zum ganz großen Teil nach dem Kormen vor. Das ist also hierher Kormen,
00:14:28
von diesen Autoren, also geschätzte 70 Prozent des Inhalts dieser Vorlesung sind aus dem Kormen und können sie da entsprechend auch nachlesen. Wenn Sie dieses Buch sich entweder ausleihen oder vielleicht sogar kaufen,
00:14:47
Dann achten Sie möglichst darauf, eine Auflage nach 2009,
00:14:53
also es ist die dritte Auflage,
00:14:54
das ist die englische Variante hier, oder die deutsche Übersetzung davon,
00:14:58
die gibt es auch, die ist dann 2010 erschienen,
00:15:02
dass sie eine von denen haben, also der Corman ist schon,
00:15:05
der hat schon eine lange Tradition, ja,
00:15:08
da hat ja auch jetzt schon die dritte Auflage,
00:15:10
das heißt, es gibt viele Bücher auch davor,
00:15:12
bei vielen Büchern ist das immer nicht so wild,
00:15:14
welche Auflage man so nimmt, ja,
00:15:16
da ändert sich dann mal,
00:15:16
das ist ja hier mal ein Tippfehler gewesen oder so,
00:15:18
und dann ist das nicht so schlimm.
00:15:20
Beim Kommen ist es aber so, dass Autoren bei
00:15:24
dem Wechsel zur dritten Auflage doch substanziell Sachen geändert haben.
00:15:28
Sie haben also zum Beispiel die Nominklatur der ganzen Pseudo-Codes geändert
00:15:34
und es wäre insofern sehr hilfreich, wenn sie ins Buch gucken,
00:15:37
in ein neues Buch zu schauen und nicht in ein altes.
00:15:39
Da kommen sie wahrscheinlich doch durcheinander im Zweifelsfall. Also wenn
00:15:42
sie sich das besorgen, schauen sie, dass sie Neues bekommen.
00:15:48
So und dann gibt es immer so ein paar Sachen,
00:15:50
die kommen einfach im Kormen leider nicht vor.
00:15:52
Also ich schätze das Buch sehr, weil das vom Aufbau her toll gemacht ist.
00:15:56
Ja, die Algorithmen sind präzise beschrieben und aber auch gut
00:16:00
begründet mit nachvollziehbaren Erklärungen und Beweisen und Beispielen,
00:16:06
aber leider ist eben nicht alles drin,
00:16:08
was meiner Meinung nach wichtig ist.
00:16:11
Und deswegen müssen wir an einer Stelle mal in so ein
00:16:14
altes kombinatorisches Optimierungsbuch reinschauen, aber das sind nur ein paar Prozent hier.
00:16:20
Und dann müssen wir uns ein bisschen umschauen im Bereich der algorithmischen Geometrie.
00:16:24
Das ist so der letzte Teil der Vorlesung.
00:16:27
Das ist so ein Gebiet, was im Kormen auch,
00:16:30
sagen wir mal, jetzt was stiefmütterlich behandelt wird.
00:16:33
Da gibt es zwar ein Kapitel zu dem Thema,
00:16:36
aber es ist nicht sehr ausführlich.
00:16:38
Deswegen haben wir da noch ein paar andere Bücher,
00:16:41
die wir angucken werden,
00:16:43
insbesondere das hier
00:16:45
Von dem Berg. Das nehme ich inzwischen ein bisschen mehr
00:16:48
als dieses Alte hier von Präparater. Ja, das ist
00:16:54
so das, was wir an Literatur haben zu dem Thema.
00:16:59
Dementsprechend liefere ich Ihnen kein Skript. Das wäre in
00:17:04
diesem Gebiet eigentlich auch wirklich nicht mehr sinnvoll,
00:17:06
weil die Lehrbücher wirklich so gut sind,
00:17:09
dass das einfach nur noch ein Kopieren wäre von Dingen,
00:17:12
die eigentlich auch schon da sind.
00:17:14
Sie können aber gerne meine Folien haben, die werden unter Stine liegen.
00:17:20
Das tun Sie im Moment gerade noch nicht, aber das wird in kürzer der Fall sein.
00:17:26
Ich werde Ihnen sozusagen die komplette Foliensammlung in einem Rutsch jetzt wahrscheinlich heute noch unterschiedene zur Verfügung stellen. Ja,
00:17:36
dann können Sie sich das runterladen,
00:17:38
vielleicht wollen Sie es ausdrucken oder so, es müssen Sie entscheiden,
00:17:41
wie Sie damit am besten umgehen und dann haben Sie quasi schon mal alles das,
00:17:43
was ich Ihnen hier an die Wand werfe und müssen das nicht in irgendeiner Art und Weise abschreiben oder so.
00:17:51
Ja, die beste Art und Weise mitzukommen und mitzuarbeiten ist meiner Meinung nach,
00:17:59
das jeder natürlich so seinen Stil und sie sind ja größtenteils im Masterstudium,
00:18:04
sie haben auch schon Erfahrungen im Studieren, aber trotzdem,
00:18:06
also meiner Meinung nach ist das Beste, was sie machen können,
00:18:09
ist tatsächlich, sich die Folien auszudrucken, müssen ja nicht,
00:18:14
können ja irgendwie vier auf eine Seite oder so und ist auch nicht so viel.
00:18:19
Und die dabei zu haben und sich dann dazu Notizen zu machen,
00:18:24
weil sie müssen immer im Kopf haben, das sind Folien,
00:18:27
die Folien enthalten natürlich auch schon relativ viel Text,
00:18:30
weil ich auch immer schon die Erklärungen dabei schreibe,
00:18:32
weil ich natürlich weiß,
00:18:33
dass viele es natürlich auch primär erst mal lesen,
00:18:36
aber trotzdem sind es eben nur Folien und es ist eben kein Skript.
00:18:40
Das bedeutet, Ich sage eine Menge Dinge, die nicht
00:18:44
auf den Folien raufstehen. Und die helfen natürlich im Nachhinein auch,
00:18:49
um die Sachen vielleicht besser zu verstehen. Und deswegen,
00:18:52
wie gesagt, meiner Meinung nach die beste Strategie,
00:18:54
nehmen sie die Folie mit und schreiben sich ein paar Sachen dazu,
00:18:57
wenn ihnen was auffällt, was ihrer Meinung nach wichtig ist,
00:18:59
was ich sage, aber was eben da nicht draufsteht.
00:19:04
Ja, das zum Thema Literatur. Okay,
00:19:10
so, Themenschwerpunkte habe ich eben schon einmal angerissen,
00:19:14
Entwurf von Algorithmen und Datenstrukturen
00:19:18
Habe eben primär über Algorithmen gesprochen. Wir werden natürlich auch
00:19:20
Datenstrukturen betrachten. Die beiden Themen hängen ja so eng miteinander zusammen,
00:19:25
dass man das eigentlich auch so gar nicht voneinander richtig trennen kann,
00:19:29
wenn man effiziente Algorithmen entwerfen will, braucht man passende,
00:19:33
effiziente Datenstrukturen und effiziente Datenstrukturen basieren in der Regel auf effizienten Algorithmen.
00:19:41
Ja, dann gucken wir uns natürlich die Beschreibung der Algorithmen an.
00:19:43
Wir wollen sie natürlich formulieren und dann analysieren wir die. Das heißt,
00:19:50
wir schauen uns zum einen natürlich erstmal die Korrektheit an,
00:19:53
das steht hier gar nicht mehr, weil der Algorithmus,
00:19:55
der hat hier nur seinen Namen und Ort in dieser Vorlesung verdient,
00:20:00
wenn er korrekt ist und wir gucken uns das natürlich an,
00:20:02
ob er das ist.
00:20:05
Und dann gucken wir uns natürlich die Platz- und Zeitkomplexität an,
00:20:08
primär die Zeitkomplexität, Platz kommt ab und zu mal vor,
00:20:12
aber sehr selten.
00:20:12
Also meistens interessieren wir uns für die Zeit. Ja,
00:20:17
und im Laufe der Vorlesung werden sie halt eine Menge Algorithmen kennenlernen,
00:20:21
für häufig auftretende Probleme. So, das sind die fünf
00:20:26
Kapitel, die wir bearbeiten werden. Wir werden anfangen,
00:20:30
also ihr steht ganz häufig weiterführend hier gerade am Anfang.
00:20:34
Das liegt daran, weil diese Vorlesung aufbaut auf
00:20:38
der Algorithmen und Datenstrukturen. Eine Vorlesung, die eigentlich,
00:20:43
also in Hamburg auf alle Fälle verpflichtend im Grundstudium ist,
00:20:47
drittes Semester, hört man Algorithmen und Datenstrukturen.
00:20:50
Und ich glaube, es gibt keinen Studiengang Informatik,
00:20:55
wo man nicht Algorithmen und Datenstrukturen irgendwann im Bachelor hört.
00:20:59
Und darauf bauen wir hier natürlich auf.
00:21:04
Wir gucken uns dann erstmal die Analyse von Algorithmen nochmal an.
00:21:11
Dann werden wir uns da an Strukturen anschauen,
00:21:13
die über die hinausgehen, die sie so im Grundstudium kennengelernt haben
00:21:18
Das Gleiche gilt für Graf-Algorithmen, eine Graf-Algorithmen im Grundstudium.
00:21:21
Da sieht man dann solche Dinge wie kürzeste Wege,
00:21:25
Berechnungen mit dem Diextra-Algorithmus oder Tiefensuche, Breitensuche.
00:21:31
Und darauf werden wir aufbauen und andere komplexere Graf-Algorithmen sehen.
00:21:37
Dann schauen wir uns Algorithmen für numerische Probleme an.
00:21:44
Da geht es primär um Fragestellungen, ja,
00:21:49
wo einfach Zahlen eine große Rolle spielen.
00:21:50
Da geht es um Optimierung primär. Das wird
00:21:53
ein kleiner Auszug sein, es ist keine Optimierungsvorlesung hier,
00:21:57
also eine numerische Optimierung
00:21:59
Aber wir werden so ein paar Dinge da eben sehen.
00:22:02
Und das fünfte Kapitel, wie gesagt, die algorithmische Geometrie,
00:22:05
wo wir uns Probleme anschauen aus der Geometrie,
00:22:09
die heute ja bei vielen Problemen auftreten.
00:22:13
Ja, also egal, ob sie heute anfangen,
00:22:15
Spiele zu programmieren oder irgendwas im Bereich der Geografie machen,
00:22:20
irgendeine neue Anwendung für Google Maps oder sonst was.
00:22:23
Sie haben so viele geometrische Fragestellungen, die immer wieder auftreten.
00:22:27
Das ist meiner Meinung nach ganz wichtig ist,
00:22:29
da mal ein paar Konzepte gesehen zu haben.
00:22:33
Okay, das ist so grob
00:22:35
die Gliederung
00:22:37
Ja, ich weiß nicht, sind einige hier die Vorlesungen
00:22:43
bei Frau von Luxburg im letzten Jahr auch gehört habe.
00:22:50
Also es sind sicherlich Dinge anders. Das sage ich gleich von vornherein. Wir haben zwar,
00:22:58
wir tauschen uns zwar aus und die Ulrike von Luxburg hat auch ursprünglich mal meine Vorlesungsunterlagen genommen,
00:23:05
als eine Basis und zu überlegen, was sie denn so macht,
00:23:07
aber sie hat zum einen andere Themenschwerpunkte gesetzt,
00:23:11
was mich unüblich ist, sind im Masterlevel da,
00:23:14
kriegen sie natürlich so ein bisschen auch die spezielleren Themen.
00:23:19
Und auch war die Vorlesung, der Übungsbetrieb ein bisschen anders.
00:23:23
Also ich werde hier im Übungsbetrieb keine Programmierung machen.
00:23:27
Das heißt, sie müssen auf den Übungszettel nichts programmieren.
00:23:31
Wir werden immer gehen bis zum Pseudo-Code-Level, aber nicht darüber hinaus,
00:23:37
weil das ist auch so eine Geschmackssache, wie man das Ganze so sieht.
00:23:42
Ich denke, es gibt genug Veranstaltungen, wo sie programmieren, gut lernen können.
00:23:46
Und das ist auch super wichtig. Aber hier,
00:23:49
es lenkt natürlich sehr schnell auch so von den Konzepten ab,
00:23:51
wenn sie sich zu sehr mit Programmierung beschäftigen,
00:23:54
um zu gucken,
00:23:54
dass es dann irgendwie läuft
00:23:56
Der Algorithmus, den sie da sehen. Das ist so eine Fragestellung,
00:24:00
aber wichtiger ist meiner Meinung nach, dass sie den Algorithmus hier wirklich verstehen.
00:24:04
Und auch dieses Arbeiten eben auf dem Papier erlernen.
00:24:08
Also das Entwerfen von Algorithmen ist primär eine Kopfsache, die,
00:24:12
naja, nach wie vor eher auf dem Papier entsteht,
00:24:16
als direkt durch Programmierung.
00:24:20
Gut. Ja, das dazu. Ich werde,
00:24:26
weil ich natürlich immer nicht so ganz genau weiß,
00:24:30
was sie vorher in Algorithmen und Datenstrukturen so gelernt haben,
00:24:37
werde ich immer so ein Rückblickenden Teil auch haben.
00:24:40
Also ich werde Dinge aus dem Grundstudium wiederholen.
00:24:45
Und das immer sozusagen an den Anfängen von den verschiedenen Kapiteln.
00:24:49
Da machen wir mal noch so einen Rückblick.
00:24:50
Meistens ist es so eine Vorlesung lang,
00:24:53
wo wir das dann nochmal Revue passieren lassen,
00:24:57
was dann gerade die Grundlage ist für das,
00:24:58
was wir als nächstes tun werden.
00:25:01
Und dann setzen wir da dann entsprechend auf. Sind hier welche,
00:25:05
die bei mir A und D gehört haben irgendwann mal?
00:25:09
War einige, okay. Also sie werden dann die Folie noch wiedererkennen,
00:25:13
wenn sie sich daran daran erinnern. Und ich hoffe,
00:25:17
dass sie sich in der kurzen Phase dann nicht so langweilen.
00:25:20
Also meistens ist es ganz hilfreich, wenn man das dann
00:25:22
einfach nochmal sieht. Weil selbst wenn man das gehört hat,
00:25:24
ist es ja schon ein bisschen her.
00:25:27
Okay, soweit der Plan. Ansonsten nur noch zum Ablauf
00:25:34
. Sie können gerne auch während der Vorlesung Fragen stellen.
00:25:40
Wenn der ein oder andere von Ihnen eine Frage hat,
00:25:43
ist es meistens ein Zeichen, dass ich es hier nicht so optimal erklärt habe.
00:25:46
Und dann haben wahrscheinlich mindestens noch 20 bis 30 Prozent mehr.
00:25:50
Eine ähnliche Frage. Deswegen ist es eigentlich ganz gut,
00:25:52
wenn Sie sie ruhig auch schon während der Vorlesung eine Frage
00:25:55
stellen und ich versuche die dann einfach direkt zu beantworten oder die Stelle einfach nochmal mit anderen Worten zu erklären.
00:26:00
Können Sie gerne machen. Im Zweifelsfall führt das dann dazu,
00:26:07
dass ich dann ein klein bisschen überziehe,
00:26:09
weil ich dann irgendwie was vorgenommen habe, was ich schaffen will.
00:26:12
Aber es sollte sie, wie gesagt, nicht davon abhalten.
00:26:15
Also Fragen zu stellen. Gut. So, damit wären
00:26:21
wir dadurch und ich würde jetzt umschalten und wir legen einfach mal los.
00:26:31
Heute wird es auf alle Fälle noch Sehr viel Wiederholung werden.
00:26:52
Okay. So, heute gibt es den ganz sanften Einstieg ins Thema.
00:26:59
Wir beschäftigen uns jetzt in dem ersten Kapitel mit der Analyse von Algorithmen.
00:27:03
Analyse von Algorithmen sollten Sie kennen aus, wie gesagt,
00:27:06
dem Grundstudium. Sie kennen hoffentlich alle die Mechanismen,
00:27:12
die man dazu hat, den mathematischen Methoden.
00:27:13
Das werden wir uns gleich noch mal ein bisschen anschauen
00:27:16
Quasi zum Warmwerden. Dann werden wir uns noch mal ganz kurz anschauen,
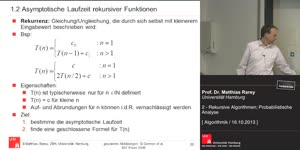
00:27:22
wie rekursive Algorithmen analysiert werden, anhand von zwei, drei Beispielen.
00:27:29
Und dann wird in diesem Kapitel, ja,
00:27:32
in der nächsten oder übernächsten Vorlesung, werden wir dann zwei andere Analysetechniken kennenlernen.
00:27:39
Und zwar die probabilistische Analyse und die amortisierte Analyse. Der Grund,
00:27:44
warum wir über das hinausgehen müssen, was wir im Grundstudium hier,
00:27:48
oder was sie im Grundstudium gelernt haben, ist,
00:27:50
dass diese Techniken, diese Analyse mit dem Worst,
00:27:53
das Worst Cases mit dem O-Kalkül Das war für die einfachen Algorithmen reicht.
00:27:58
Aber wenn sie so richtig noch was aus der Komplexitätsschranke rauskitzeln wollen,
00:28:06
dann sind die einfach nicht mehr gut genug, diese Analysen.
00:28:10
Und deswegen müssen wir uns zum Beispiel mit dem Average Case auseinandersetzen.
00:28:13
Also wie analysieren wir den mittleren Fall der Laufzeit eines Algorithmus?
00:28:18
Was tun wir, wenn unser Algorithmus Zufallszahlen verwendet?
00:28:21
Für diese beiden Konzepte brauchen wir die probabilistische Analyse. Und ja,
00:28:28
dann haben wir ab und zu die Situation,
00:28:31
dass wir in dem klassischen Worst Case Szenario zu grob abschätzen,
00:28:38
weil wir immer für jeden Teil eines Algorithmus den ungünstigsten Fall annehmen.
00:28:43
Da kommt eine Vorschleife und dann sagen wir, ja,
00:28:44
die wird mindestens so häufig durchlaufen und dann kommt danach noch eine Vorschleife,
00:28:47
dann sagen die wird mindestens so häufig durchlaufen und dann nehmen wir immer den Worst Case,
00:28:50
Worst Case, Worst Case und dann kommt eine relativ große Schranke raus.
00:28:55
Die müsste vielleicht gar nicht so groß sein,
00:28:57
wenn wir ein bisschen genauer hinschauen,
00:29:00
wie häufig zum Beispiel Schleifen wirklich durchlaufen werden und wenn wir
00:29:03
so ein bisschen austarieren zwischen verschiedenen Funktionsaufrüfen und so eine,
00:29:08
vielleicht eine Gesamtbetrachtung machen.
00:29:10
Sowas macht man in der amortisierten Analyse.
00:29:13
Das werden wir dann
00:29:14
Auch noch sehen. Okay, so, der Anfang wird
00:29:19
also gleich ein bisschen steinig, sage ich ganz ehrlich.
00:29:23
Aber wenn wir das hier hinter uns haben,
00:29:25
haben wir so ein bisschen das Rüstzeug und können dann
00:29:27
richtig loslegen und werden dann also in den Graf-Algorithmen einsteigen.
00:29:31
Und das wird uns dann auch sehr lange hier erstmal beschäftigen.
00:29:36
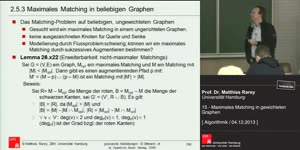
Okay, so. Hier sind erstmal unsere zentralen Begriffe in
00:29:41
der Algorithmik, wovon reden wir?
00:29:43
Wir reden von Problemen von Instanzen, von Algorithmen und von Korrektheit
00:29:49
. Und dabei meinen wir ganz spezielle Dinge.
00:29:51
Es ist immer wichtig, das zu sagen,
00:29:53
weil diese Therme ja
00:29:54
auch in unserem normalen Sprachgebrauch vorkommt
00:29:58
Also, ein Problem ist für uns immer definiert durch eine
00:30:01
ganz konkrete Eingabe, Ausgabebeziehung. Ja, das heißt,
00:30:05
wenn wir von einem Problem reden, hier in dieser Vorlesung,
00:30:08
dann ist es schon ein formalisiertes Problem, wo klar ist,
00:30:12
das ist die Eingabe und das ist das erwartete Resultat und die Spezifikation ist eben so,
00:30:19
dass die Ausgabe eben eindeutig aus der Eingabe hervorgeht.
00:30:24
Jedes Problem hat dann Instanzen,
00:30:26
eine Instanz kann man sich einfach so vorstellen,
00:30:28
dass es eine mögliche Eingabe ist für das Problem und die Instanzen sind ganz wichtig,
00:30:33
weil wenn wir die analysieren wollen,
00:30:35
dann hängt die natürlich eigentlich von der Eingabe ab.
00:30:38
Und deswegen müssen wir uns immer mit den möglichen Eingaben
00:30:40
für so ein Problem beschäftigen. Das sind die Instanzen.
00:30:43
Der Algorithmus ist einfach, ja, kennen Sie schon,
00:30:49
die Folge von Anweisungen zur Lösung des Problems.
00:30:53
Hier stehen nochmal die wichtigsten Eigenschaften von Algorithmen, mechanisch ausführbar.
00:30:57
Das heißt, jeder Schritt ist ausführbar ohne eine weitere,
00:31:02
sagen wir mal, intellektuelle Interpretation.
00:31:07
Der Algorithmus besteht aus mehreren elementaren Schritten,
00:31:10
das ist also aus Schritten zusammengesetzt,
00:31:12
aus einer Sequenz von Schritten
00:31:14
Die wesentlichen Konzepte, die wir haben,
00:31:17
um einen Kontrollfluss in einem Algorithmus zu konzipieren,
00:31:20
also um zu entscheiden, welche Schritte als nächstes ausgeführt werden,
00:31:23
sind die Iterationen, also die wiederholte Ausführung einzelner Schritte,
00:31:27
die Selektion.
00:31:28
Das heißt, die bedingte Ausführung einzelner Schritte und die Rekursion.
00:31:32
Das heißt, die Ausführung des Verfahrens mitgeänderten Eingabeparametern.
00:31:37
Daraus bestehen unsere Algorithmen und aus mehr auch eigentlich nicht.
00:31:42
Ja, die Korrektheit müssen wir zeigen
00:31:48
Bei der Korrektheit ist es zu beachten,
00:31:50
dass ein Algorithmus nicht nur die korrekte Ausgabe produzieren muss.
00:31:54
Er muss auch halten, sonst ist er nicht korrekt.
00:31:56
Das ist etwas, was aus dem Begriff vielleicht als erstes nicht so hervorgeht.
00:32:01
Also ich meine, klar muss der irgendwie halten,
00:32:02
weil wenn er nicht anhält, dann kann er ja kein Ergebnis produzieren.
00:32:05
Aber wenn sie nachweisen, dass sie Algorithmus korrekt ist,
00:32:08
dann gehört dazu eben auch, dass sie zeigen,
00:32:11
dass der Algorithmus für jede mögliche Eingabe auch hält.
00:32:16
Das müssen sie also im Prinzip auch zeigen,
00:32:18
dass das so ist
00:32:20
Es ist ganz, ganz selten, dass das tatsächlich ein Problem ist.
00:32:23
Die Algorithmen, die wir ja alles sehen werden,
00:32:25
da ist es ganz offensichtlich, dass die halten werden.
00:32:27
Die haben einfach nur so Schleifen. Und dann sehen sie sofort,
00:32:29
ah ja, klar,
00:32:30
es läuft jetzt ja endmal oder irgendwas und dann ist Schluss.
00:32:34
Aber es ist wichtig, dass man einfach darauf hinweist,
00:32:36
dass es ein Bestandteil ist der Korrektheit, das Algorithmen eben halten.
00:32:43
Gut, wie beschreiben wir Algorithmen? Dazu haben wir in
00:32:49
der Informatik eine ganze Reihe von Möglichkeiten.
00:32:53
Wir werden uns hier auf Pseudocode konzentrieren, aber damit man
00:32:56
einfach mal alles sieht.
00:32:58
Wir haben die natürliche Sprache
00:33:00
Wir können Algorithmen einfach verbal kommunizieren. Ja, das machen wir
00:33:05
den lieben langen Tag, was wir Algorithmen verbal kommunizieren.
00:33:08
Wir geben Handlungsanweisungen an irgendjemanden und solange die,
00:33:12
oder sobald die mehr als einen Schritt enthalten,
00:33:14
das ist streng genommen ein Algorithmus, ja.
00:33:16
Natürliche Sprache ist für uns allerdings zu unpräzise,
00:33:22
weil wir natürlich aus dem Umgang mit natürlicher Sprache schon wissen,
00:33:26
die natürliche Sprache ist voll von den Möglichkeiten, Missverständnisse zu produzieren.
00:33:31
Und das macht unser Leben spannend,
00:33:32
aber wenn man mit Computern und solchen Problemen arbeitet,
00:33:35
ist es meistens eher hinderlich.
00:33:37
Das heißt, wir werden natürliche Sprache natürlich hier nicht verwenden
00:33:41
Das andere Extremum ist ein Computerprogramm, also die Software,
00:33:45
die Software beschreibt, Algorithmen eigentlich schon vollständig und sogar sehr präzise und genau.
00:33:53
Allerdings hängt das von so vielen Details ab.
00:33:56
Welche Programmiersprache verwenden Sie, vielleicht sogar welcher Computer wird verwendet?
00:34:02
Und das sind also die Details, die ja für
00:34:03
das Verständnis des Algorithmus gar nicht so wichtig sind.
00:34:07
Das macht die Computerprogramme wieder so ein bisschen unattraktiv,
00:34:11
um Algorithmen zu beschreiben. Also es ist aufwendig,
00:34:14
das zu lesen, sehr viele Detailsachen,
00:34:16
was wir nicht brauchen
00:34:20
Der dritte Teil ist Hardwareentwurf,
00:34:22
also auch Hardwareentwurf ist eine Beschreibungsform für Algorithmen,
00:34:25
das werden wir hier in der Vorlesung nicht weiter betrachten,
00:34:30
aber wenn sie in Vorlesungen denken, wie zum Beispiel Rechnerarchitektur,
00:34:35
haben sie wahrscheinlich auch irgendwann mal gehört in ihrem Studium,
00:34:39
dann werden da Komponenten besprochen,
00:34:41
die in Hardware realisiert werden und auch die folgen natürlich Algorithmen.
00:34:46
Was wir eben machen werden,
00:34:48
hier ist die Mischung aus 1 und 2,
00:34:50
das heißt natürlicher Sprache und Pseudo und Computerprogramme und auf
00:34:55
diese Art und Weise werden wir zum Pseudo-Code kommen,
00:34:59
was sich einfach durchgesetzt hat in der Algorithmen Forschung und Entwicklung und auch in den Textbüchern.
00:35:05
Ja, wenn Sie also Algorithmenbüchern lesen, sind die
00:35:07
immer voll von Pseudocode, um die Verfahren zu erklären.
00:35:10
Und das ist auch super, weil die kann man
00:35:13
schnell lesen, die kann man schnell verstehen.
00:35:15
Also es ist auf das Wesentliche reduziert. Und trotzdem sind
00:35:18
sie eben präzise. Und man weiß genau, was man
00:35:21
zu tun hat, wenn man jetzt tatsächlich diesen Algorithmus mal umsetzen möchte.
00:35:29
Okay, Beschreibung von Algorithmen sind wie auch Spezifikationen vollständig detailliert und unzweideutig.
00:35:36
Und hier ist so ein bisschen ein Problem bei dem Pseudocodes.
00:35:39
Hier muss man aufpassen
00:35:41
Denn durch diese Mischung mit der natürlichen Sprache passiert es einem manchmal,
00:35:45
dass er eben nicht so ganz unzweideutig,
00:35:48
also eindeutig ist, wenn sie so wollen.
00:35:51
Oder dass er auch nicht ganz vollständig ist,
00:35:53
weil man einfach vielleicht eine Bedingung als Textfragment irgendwie formuliert.
00:35:59
Darauf muss man sehr achten, wenn man Pseudocode formuliert,
00:36:04
dass diese Regeln auf alle Fälle gelten.
00:36:07
Und die Kunst ist so ein bisschen genau das richtige Niveau zu finden,
00:36:11
wenn man einen Pseudocode aufschreibt, dass er eben diese Eigenschaften hat,
00:36:16
was er wirklich eindeutig ist und nicht missverstanden oder falsch interpretiert werden kann.
00:36:21
Und trotzdem eben möglichst knapp und prägnant und kurz
00:36:27
Pseudo-Code, da gibt es eigentlich keine echte Konvention.
00:36:31
Das ist in der Regel immer angelehnt an imperative Programmiersprachen.
00:36:35
Je nachdem, aus welcher Generation so das Buch stammt,
00:36:38
eben so Pascal-ähnlich oder ja, war ähnlich oder C ähnlich.
00:36:43
Da gibt es also immer so Varianten. Und die Art und Weise,
00:36:49
wie es gemacht wird, ist, dass die Kontrolle und Datenstrukturen,
00:36:51
das wird so ein bisschen aus den Programmiersprachen übernommen.
00:36:54
Da steht dann also ein Wild und ein If und so.
00:36:58
Aber Bedingungen, Funktionen, also gerade Funktionen,
00:37:01
wo eigentlich klar ist, was dort gemacht werden muss,
00:37:05
die werden dann je nach Kontext umgangssprachlich dann definiert,
00:37:10
um das Ganze entsprechend zu vereinfachen
00:37:14
Ja, wir werden hier den Pseudo-Code aus dem Kormen verwenden.
00:37:22
Den habe ich hier noch mal zusammengefasst. Und zwar ist
00:37:25
das die Pseudo-Code-Konvention aus dem Kormen ab der dritten Auflage.
00:37:30
Deswegen ist es noch mal so wichtig mit der Auflage.
00:37:33
Das hat sich nämlich komplett geändert von den vorherigen Auflagen.
00:37:41
Ich habe mir die Mühe gemacht und hoffe,
00:37:43
dass ich es jetzt auch vollständig geschafft habe,
00:37:46
wirklich jeden Pseudo-Code, der in dieser Vorlesung kommt,
00:37:49
nach dieser Spezifikation aufzuschreiben,
00:37:52
auch wenn er nicht aus dem Kormen stammt
00:37:53
Und viele sind nicht aus dem Kormen,
00:37:55
selbst wenn das Thema im Kormen so drin ist.
00:37:59
Und das macht es für sie ein bisschen einfacher,
00:38:00
weil es einfach immer die gleiche Struktur hat.
00:38:05
Und ich würde sie einfach bitten in den Übungen,
00:38:09
sich auch an diese Konventionen zu halten.
00:38:13
Das ist nicht schwer. Das ist meistens nur eine Frage,
00:38:17
sagen wir mal, naja, man muss dann einmal genau hingucken,
00:38:19
wie ist es denn da gemacht und so mache ich es halt auch.
00:38:23
Und das hat einfach den Vorteil,
00:38:26
dass wir da keine Missverständnisse haben,
00:38:28
insbesondere auch in dem Übungsbetrieb,
00:38:31
wenn sie Sachen vorstellen,
00:38:32
dann können die anderen
00:38:33
das wieder leichter verstehen
00:38:34
Und die Übungsgruppenleiter können es auch ein bisschen leichter verstehen, was sie gemeint haben.
00:38:39
Also halten Sie sich bitte möglichst an diese Konventionen aus dem Kormen.
00:38:44
Hier sind Sie ganz knapp zusammengefasst im Kormen. Du könntest
00:38:46
es auch ein bisschen genauer nachlesen. Wir haben eine Blogstruktur,
00:38:52
wie wir sie aus imperativer Programmierung kennen. Wir haben keine Klammern,
00:38:56
sondern wir rücken entsprechend die Blöcke ein und markieren dadurch quasi die Blogstruktur.
00:39:02
Es gibt mittlerweile Skriptsprachen, die sowas auch entsprechend machen. Dann haben wir natürlich ein If-Ls,
00:39:11
was sich ja an so ein bisschen an C anlehnt,
00:39:16
ja, das heißt, wir haben IF, dann haben wir Runde Klammern,
00:39:19
da drinnen steht die Bedingung und dann fängt dann der Blog an,
00:39:25
wo dann der Coach steht ja zu der Bedingung gehört,
00:39:28
der dann ausgeführt werden soll,
00:39:29
wenn die Bedingung wahr ist und dann können sie noch ein Els dahinter schreiben.
00:39:35
Es gibt auch die Möglichkeit, ein Els IF zu machen,
00:39:37
um das Ganze so ein bisschen zu verkürzen,
00:39:39
aber streng genommen ist es eigentlich nicht nötig,
00:39:41
ich benutze das eigentlich auch nicht,
00:39:42
weil es das auch in dem Programm meisten Programmiersprachen in dieser
00:39:45
Form nicht gibt und man sowieso ein getrenntes Els und dann
00:39:47
IF schreibt,
00:39:51
um das dann aufzuschreiben
00:39:53
Hier steht kein Denn, ja, was man häufiger mal
00:39:56
im Pseudo-Code sieht. Hier ist es, wie gesagt,
00:39:58
angelehnt an C und da tritt dann eben einfach nur Digit.
00:40:03
Sind nur die Klammern da. Im Kormen sind auch diese Klammern
00:40:06
noch nicht mal verpflichtend. Da steht dann einfach nur If
00:40:09
und dahinter steht dann die Bedingung. Ich habe bei mir versucht,
00:40:12
weil ich es einfach, ich habe das dann gemerkt,
00:40:14
als ich meinen Pseudo-Code umformuliert habe, dass das doch wesentlich übersichtlicher ist,
00:40:18
wenn die Bedingungen wirklich immer in runden Klammern ist.
00:40:21
Und also ich habe das versucht, einigermaßen konsistent zu machen.
00:40:24
Gleiches gilt für Schleifen, ja, die ich
00:40:26
auch immer konsequent klammere hier
00:40:30
Gut, es gibt also eine Wildschleife, eine Vorschleife,
00:40:34
eine Repeat an Tillschleife, die natürlich auch relativ selten ist.
00:40:40
Und die sehen eben so aus, ein Wild und dann in runden Klammern eine Bedingung.
00:40:44
Und wenn die wahr ist, wird halt der Schleifenrumpf ausgeführt,
00:40:46
eine Vorschleife mit einem Iterator hier in der Variablen,
00:40:50
die eben von einem Wert oder Ausdruck hochgezählt wird zu einem anderen Wert.
00:40:56
Hier können sie sich statt dem Two auch ein Down-Two machen,
00:40:58
wenn sie mal ein rückwärtiges Zählen beschreiben müssen.
00:41:04
Und wenn man tatsächlich mal eine Situation hat, dass man,
00:41:08
dass es sich um größere Werte inkrementieren muss,
00:41:10
dann kann man das natürlich streng genommen auch annotieren,
00:41:12
was natürlich jetzt so erstmal hier jetzt nicht vorgesehen ist,
00:41:15
aber da findet sich dann echt ein Weg.
00:41:17
Dann kommen hier die Anweisungen, Repeat an Tills,
00:41:20
einfach nur die Schleife mit der Bedingung am Ende.
00:41:23
Das ist der einzige Unterschied. Dann vielleicht bei den Schleifen noch der Hinweis,
00:41:30
also insbesondere bei der Vorschleife,
00:41:34
dass hier auch die C-Konvention gilt,
00:41:36
das bedeutet,
00:41:38
dass auch nach Schleifenende die Schleifenden Iteratorvariable definiert ist und
00:41:44
dann entsprechend Untertitel der Amara.org-Community Einfache gleich für die Zuweisung
00:42:38
Und hat die eckigen Klammern auf so Attribute verwendet. Das war sehr,
00:42:41
sehr ungewöhnlich, weil man ja schon den C,
00:42:47
aber spätestens nach der Objektorientierung Attribute einfach immer mit dem Punktoperator trennt.
00:42:52
Und das ist heute auch so. Also hier ist dann der Punktoperator,
00:42:56
mit dem man dann einen Attribut eines Objekts beschreiben kann.
00:43:00
Also wenn man zum Beispiel einen Array hat,
00:43:02
A und man will die Länge des A-Rays beschreiben,
00:43:04
dann schreibt man A. längs.
00:43:09
Funktionsparameter werden Call by Value übergeben, grundsätzlich erstmal,
00:43:15
also auch genau wie in C. Aber es ist ja auch so,
00:43:19
dass Objekte und Array bezeichnen immer Adressen von Objekten beschreiben,
00:43:23
also das eigentlich ein Call by Reference ist.
00:43:29
Ich habe an ein oder anderen der einen oder anderen Stelle einen Pseudo-Code,
00:43:33
wo ich dezidiert einen Call by Reference brauche und da mache ich das dann so,
00:43:37
wie sie das zum Beispiel aus C plus kennen,
00:43:40
dass man explizit den Parameter oder den Funktionsparameter markiert
00:43:45
als Adresse oder Pointer
00:43:49
Gut. Ja, letzter Punkt ist die Auswertung von bullischen Operatoren.
00:43:54
Wenn Sie also und oder oder in Bedingungen haben,
00:43:59
dann kommt es zu einer sogenannten trägen Auswertung.
00:44:02
Das heißt Lazy evaluation auf Neudeutsch. Das bedeutet, dieser Ausdruck,
00:44:07
der wird von links nach rechts ausgewertet und zwar nur so lange,
00:44:10
bis feststeht, ob der Ausdruck war oder falsch ist.
00:44:13
Und dann wird die Auswertung abgebrochen. Das heißt,
00:44:17
wenn Sie X und Y lesen,
00:44:19
dann wird Y nur ausgewertet, wenn X wahr ist.
00:44:21
Ja, weil wenn X falsch ist,
00:44:23
dann wissen Sie schon,
00:44:23
der Ausdruck kann sowieso nicht mehr wahr werden,
00:44:25
dann wird Y
00:44:25
nicht mehr ausgewertet
00:44:27
Und das Gleiche gehst bei Ola, bei X und X oder Y
00:44:31
wird Y nur ausgewertet, wenn X falsch ist.
00:44:34
Weil wenn X wahr ist, ist der Therm sowieso wahr
00:44:36
und dann muss der zweite Teil nicht ausgewertet werden.
00:44:40
Da fragen sich jetzt wahrscheinlich, mein Gott,
00:44:42
wir schreiben doch hier Pseudo-Codes, das ist doch völlig egal,
00:44:45
ob das noch ausgewertet wird oder nicht.
00:44:47
Das ist natürlich häufig egal, aber nicht immer,
00:44:52
weil der zweite Teil einer solchen Bedingung kann ja zum Beispiel
00:44:55
ein Funktionsaufruf sein mit einer relativ hohen Laufzeit.
00:45:01
Dahinter kann sich eine Funktion verbergen, die viel Zeit benötigt.
00:45:04
Und dann ist es eben entscheidend,
00:45:05
auch schon auf der Ebene des Pseudo-Codes,
00:45:08
ob dieser Therm noch ausgewertet wird oder nicht
00:45:13
Ja, das ist so alles für die Beschreibung von Algorithmen, so wie wir sie hier halt in der Vorlesung verwenden werden. Okay,
00:45:24
Beispiel, hier ist es eine textuelle Beschreibung des GGT-Algorithmus,
00:45:29
iterative Variante würde so aussehen, also Bezeichnung der Funktionswahl Parameter,
00:45:36
eine Wildschleife in runden Klammern, das Kriterium,
00:45:38
Amodolo B muss größer sein als Null,
00:45:40
wenn das der Fall ist,
00:45:42
wird der Rest auf Amodolo B gesetzt und dann kriegt A den Wert von B und B den Wert von R und solange diese Bedingungen noch wahr ist,
00:45:50
wird die nächste Schleife da durchlaufen und wenn das B,
00:45:54
wenn ein A-Modolo B, irgendwann mal ein Null ist,
00:45:56
dann wird B zurückgegeben, ist die Art und Weise,
00:45:59
wie wir nach Euklid, dem größten gemeinsamen Teiler berechnen können.
00:46:03
Natürlich können wir es auch rekrusiv machen, rekrusive Beschreibung,
00:46:06
sehe eben so aus,
00:46:07
dass man den Rest berechnet als A-Modolo B,
00:46:10
wenn der Rest größer ist als Null,
00:46:11
rufen wir rekrusiv die Funktion auf mit den Parametern B und R und anderenfalls geben wir einfach B zurück.
00:46:20
Pseudokurs, diese Art, wenn wir auch ganz,
00:46:22
ganz viele sehen im Laufe der Vorlesung.
00:46:26
Gut, so, wie funktioniert die Analyse von Algorithmen für uns?
00:46:32
Also unser Ziel ist es, ohne ein Programm zu schreiben,
00:46:38
eine Abschätzung zu bekommen, wie effizient ein Verfahren ist,
00:46:41
damit wir verschiedene Verfahren vergleichen können.
00:46:44
Algorithmen analysiert man aus verschiedensten Gründen. Die Situation ist eigentlich
00:46:51
immer die gleiche. Wir haben irgendein Problem und das Problem
00:46:55
hat eine natürliche Komplexität, kann man sagen.
00:46:59
Also man wird eine gewisse Zeit benötigen, um dieses Problem zu lösen.
00:47:03
Aber wie diese Zeit, also wie viel Zeit wir benötigen,
00:47:06
ist in der Regel unbekannt.
00:47:08
Selbst für einfache Probleme wissen wir das erstmal in der Regel nicht.
00:47:12
Wie viel Zeit wird benötigt
00:47:14
Für die meisten Probleme ist es auch extrem schwer, das herauszufinden.
00:47:18
Und wir werden es hier auch nur für ganz,
00:47:21
ganz wenige Probleme herausfinden. Was die wirkliche Zeit ist,
00:47:26
die man braucht, um das Problem zu lösen.
00:47:29
Was stattdessen passiert ist, dass sie einen Algorithmus entwerfen.
00:47:33
Sie entwerfen einen Algorithmus und sagen, damit könnte ich das Problem lösen.
00:47:38
Und dieser Algorithmus, dann zeigen sie, der ist korrekt,
00:47:40
sonst wäre es kein Algorithmus für das Problem.
00:47:42
Und für den Algorithmus können sie eine Laufzeit bestimmen.
00:47:46
Die kann auch relativ exakt sein, diese Laufzeitbeschreibung.
00:47:49
Und trotzdem ist das immer nur eine obere Schranke,
00:47:52
Für die Laufzeit, die sie benötigen, um das Problem zu lösen.
00:47:55
Weil es ist ja die Laufzeit für diesen Algorithmus.
00:47:57
Es kann ja noch einen anderen Algorithmus geben, der das Problem effizienter schneller löst.
00:48:03
Okay, das ist also die obere Schranke hier.
00:48:05
Und dann würden sie mit vielleicht einem besseren Algorithmus diese Oberschranke
00:48:10
entsprechend erniedrigen. Und sich wahrscheinlich der tatsächlichen Laufzeit,
00:48:16
diese Benötigung, das Problem zu lösen, irgendwie annähern.
00:48:20
Das Problem bei der ganzen Geschichte ist, wir wissen nie,
00:48:22
ob es sich lohnt, noch einen effizienteren Algorithmus zu suchen.
00:48:27
Weil es könnte ja sein, dass wir hier schon angekommen sind,
00:48:30
Wir haben aber nur die Bestätigung, dass wir wissen,
00:48:33
wie lange es dauert, das Problem mit diesem Algorithmus zu lösen.
00:48:35
Und wir wissen häufig nicht, ob es einen effizienteren Algorithmus gibt.
00:48:40
Die einzige Möglichkeit, da Gewissheit zu bekommen,
00:48:43
ist mit einer unteren Schranke, also eine untere Schranke anzugeben,
00:48:47
wie viel Zeit man denn mindestens benötigt, um das Problem zu lösen.
00:48:51
Untere Schranken sind sehr, sehr schwer zu finden und zu beweisen,
00:48:56
dass die korrekt sind,
00:48:58
weil eine untere Schranke muss ja quasi jeden möglichen Berechnungsweg berücksichtigen,
00:49:05
egal wie sie es machen,
00:49:06
die Laufzeit muss mindestens so und so groß sein.
00:49:08
Das ist die Aussage,
00:49:09
die sie treffen
00:49:11
Und dahinter verbirgt sich so ein für alle, so ein berühmter Allquantor.
00:49:15
Für alle Algorithmen wissen wir oder wollen wir zeigen,
00:49:19
die Laufzeit ist mindestens so groß. Und Allquantoren sind immer unangenehm,
00:49:23
wenn man etwas für alle beweisen muss, dann wird das schwierig.
00:49:26
Und so ist es hier auch bei den Schranken. So,
00:49:29
dass wir zwar meistens, wir kennen meistens ein relativ triviale untere Schranke,
00:49:34
zum Beispiel bei den allermeisten Problemen können sie sagen,
00:49:36
naja, sie müssen wenigstens mal den Input lesen.
00:49:39
Das heißt, die Laufzeit ist mindestens mal proportional zur Größe der Eingabe.
00:49:43
Das ist sie meistens so eine triviale untere Schranke,
00:49:46
die können sie immer angeben. Naja, und Von der
00:49:50
können Sie sich dann vielleicht hocharbeiten und genauere untere Schranken angeben.
00:49:55
Wir werden hier unter Schranken eigentlich, ich weiß gar nicht,
00:49:58
für nur sehr wenige Probleme sehen.
00:49:59
Und das sind tendenziell auch eher triviale untere Schranken.
00:50:03
Sie kennen bestimmt die untere Schranke für das Sortieren durch Vergleichen
00:50:07
. Das ist also die untere Schranke,
00:50:09
die man so in Algorithmen und Datenstrukturen kennenlernt,
00:50:11
wo man dann zeigt, dass wenn man Sortieralgorithmen entwirft,
00:50:15
die über Vergleiche, also ein paar Vergleiche von Elementen arbeiten,
00:50:19
dass die mindestens eine Laufzeit von N-Login haben werden.
00:50:25
Ja, okay, also das ist unser Ziel,
00:50:26
uns hier anzunähern von beiden Seiten und möglichst effiziente Algorithmen
00:50:30
zu finden
00:50:32
Gut, zunächst mal zur Korrektheit. Hier nochmal
00:50:36
eine Wiederholung, wie wir Korrektheit zeigen. Normalerweise,
00:50:42
wenn man es ganz vollständig macht, würde man
00:50:44
eine Vor- und eine Nachbedingung für jede Anweisung eines Pseudocodes angeben.
00:50:49
Das wäre eine präzise, formaler Korrektheitsbeweis. Ja,
00:50:54
Sie sagen immer, was gilt vor einer Anweisung?
00:50:55
Was gilt nach einer Anweisung? Das machen Sie Zeile für
00:50:58
Zeile. Und wenn Sie extrem sicherheitskritischen Code entwickeln,
00:51:03
dann ist es manchmal auch so, dass man wirklich so vorgeht.
00:51:07
Für die allermeisten Algorithmen ist das viel zu aufwendig und auch
00:51:10
nicht notwendig
00:51:12
Was wir in der Regel machen, ist,
00:51:14
also für viele Anweisungen ist es eigentlich klar.
00:51:15
Also wenn wir so eine Zuweisung haben wie hier, ist völlig klar,
00:51:19
was da passiert. Und dementsprechend ist das da gar nicht nötig,
00:51:24
dass man sich hier mit der Vor- und Nachbedingungen genau auseinandersetzt.
00:51:31
Schwieriger ist es schon in Schleifen, so wie hier,
00:51:33
wenn man jetzt so eine Schleife hat,
00:51:35
weil für eine Schleife muss man ja irgendwie die Korrektheit,
00:51:40
ja, durch diese Schleife hindurch transportieren,
00:51:43
wenn man so will.
00:51:45
Es gibt auch eine Fortenne Nachbedingung hier,
00:51:47
aber dieser Code wird ja mehrfach durchlaufen und dadurch ändern sich
00:51:50
ja auch Vor- und Nachbedingungen immer wieder
00:51:54
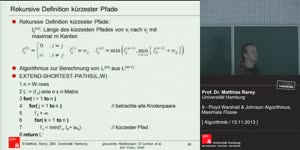
Ja. Die Art und Weise,
00:51:55
wie man das macht, ist durch eine sogenannte Schleifen-Innen-Variante.
00:51:58
Das heißt, man beschreibt einen logischen Ausdruck,
00:52:02
also einen Ausdruck, der wahr oder falsch ist,
00:52:06
der sowohl Vorausführung als auch Nachausführung jeder Iteration als auch am Ende der Schleife gilt.
00:52:13
So eine Innenvariante muss man finden, um die Korrektheit
00:52:16
eines Algorithmus zu zeigen, der eine Schleife enthält.
00:52:20
Das Finden von solchen Innenvarianten kann ganz schön tricky sein.
00:52:25
Das ist manchmal nicht trivial, darauf zu kommen, wie
00:52:29
diese Innenvariante aussehen muss. Im Grundstudium haben sie und Datenstrukturen
00:52:32
sicherlich auch schon im Reihe von Innenvarianten gesehen.
00:52:35
Manchmal beschreiben die nur textuell so das,
00:52:38
was der Algorithmus tut, dann ist es nicht so schwer.
00:52:40
Und manchmal, gerade bei so mathematischeren Verfahren wie hier,
00:52:44
wo es einfach um die Berechnung der Potenz geht,
00:52:46
ist es schwieriger, so eine Innenvariante zu formulieren.
00:52:49
Hier ist natürlich noch ganz einfach. Also hier haben wir
00:52:52
einen Pseudo kurz zur Berechnung von A hoch K. Ja,
00:52:56
das machen wir einfach, indem wir in einer Variablen B
00:52:59
den Wert 1 reinschreiben und dann kam mal den Wert A da drauf multiplizieren,
00:53:03
also ein ganzes trivialer Algorithmus.
00:53:06
Und eine Innenvariante hier sehe so aus,
00:53:08
dass wir nach I-Iterationen das natürlich schon I mal gemacht haben dementsprechend der Wert B,
00:53:15
oder der Wert der Variablen B, dem Wert A hoch I entsprechen muss.
00:53:19
Und wenn wir dann diese K-Durchläufe hier gemacht haben,
00:53:22
dann ist der Wert von B dann auch K. Ja, okay.
00:53:30
So, das muss ich gerade mal gucken.
00:53:37
Das zur Korrektheit. Wir werden gleich nochmal uns nochmal mit
00:53:43
dem Potenzalgorithmus hier beschäftigen und eine andere Variante davon sehen.
00:53:47
Und da werden wir dann auch sehen,
00:53:48
dass die Innenvariante eben nicht mehr ganz so trivial ist.
00:53:55
Wir kennen sie auch. Physikalische Laufzeit wäre natürlich schön,
00:53:58
wenn wir wirklich sagen könnten, der Algorithmus,
00:54:00
die Eingabe dauert so und so viele Millisekunden.
00:54:02
Können wir natürlich nicht. Aus ganz vielen Gründen,
00:54:04
typischerweise wissen wir nicht, auf welchem Computer das läuft,
00:54:08
welche Taktfrequenz der hat, welche anderen parallelen Jobs noch laufen.
00:54:12
Es gibt so viele Kriterien, warum wir
00:54:14
nicht physikalische Laufzeit bestimmen können. Und abhängig von dem,
00:54:20
unabhängig von dem Computer, haben wir auch das Problem,
00:54:22
dass die physikalische Laufzeit von vielen Details der Eingabe abhängt.
00:54:27
Also ich kann nicht sagen,
00:54:28
dass das Sortieren von zehn Zahlen so und so viele Sekunden oder Millisekunden dauert,
00:54:33
weil eine andere Folge von zehn Zahlen kann eben länger dauern
00:54:36
als die eine Zahlenfolge,
00:54:38
die ich mir da gerade angeschaut habe
00:54:40
Deswegen machen wir ein paar Modellannahmen. Wir gehen von
00:54:43
einem Uniform-Kostenmaß aus. Das heißt, wir sagen mal,
00:54:47
dass die mathematischen Operationen unabhängig von der Größe der Parameter nichts kosten oder nichts.
00:54:53
Also eine konstante Zeiteinheit kosten. Das geht so lange gut,
00:54:57
wie unsere Zahlenwerte in einem sinnvollen Zahlenbereich sind.
00:55:01
Wenn die groß werden, dann muss man aufpassen.
00:55:04
Also gerade, wenn sie so an kryptografische Verfahren denken,
00:55:09
können sie nicht mehr mit dem Uniformen Kostenmaß arbeiten. Wenn sie sagen,
00:55:13
ich muss da hier mal irgendwelche Divisionen machen und sie haben 500,
00:55:16
600-stellige Zahlen, dann können sie nicht mehr davon ausgehen,
00:55:19
dass es ihn konstant hat
00:55:20
Aber für das, was wir hier sehen, ist das
00:55:21
in der Regel okay. So, und dann haben wir
00:55:25
ein RAM-Modell im Hintergrund, RAM-Abkürzung für random Access Machine.
00:55:29
Das heißt, der Zugriff auf Daten kostet konstante Zeit.
00:55:33
Wir können auf jedes Datenelement beliebig zugreifen. Die Algorithmen werden
00:55:37
sequenziell ausgeführt. Wir werden hier keine parallele Algorithmik machen.
00:55:41
Ist auch ein ganz tolles Gebiet der Informatik, machen wir hier aber nicht.
00:55:45
Also gucken wir uns immer nur an sequenziellen Ablaufen,
00:55:47
Algorithmen an. Wir geben keine exakten Laufzeiten an,
00:55:52
sondern nur Schranken und wir vernachlässigen konstante Faktoren.
00:55:57
Und ja, Das sind sozusagen die zentralen Annahmen,
00:56:00
die uns dann als nächstes auch dann natürlich zum O-Kalkül führen,
00:56:04
um die Laufzeiten korrekt zu beschreiben.
00:56:07
Speicherplatz gibt es im Rahmenmodell auch eine wichtige Annahme, nämlich,
00:56:12
dass Datenobjekte, also elementare Datenobjekte in konstant viel Speicher gespeichert werden können,
00:56:18
unabhängig von der Größe des Zahlenwerts.
00:56:20
Das war so eine Analogie zu diesem Uniformkostenmaß hier oben bei der Laufzeit.
00:56:24
Das heißt, egal wie groß die Zahl ist,
00:56:27
sie können immer davon ausgehen, sie können das in einer Speicherzelle speichern.
00:56:31
Auch das ist natürlich eine Annahme,
00:56:34
die natürlich praktisch nicht korrekt ist,
00:56:36
aber für die Analysen,
00:56:37
die wir hier machen in der Regel,
00:56:38
völlig ausreichend ist
00:56:42
So, wenn wir jetzt die Effizienz bewerten wollen,
00:56:47
dann hängt die Effizienz des Algorithmus eben natürlich von dem Algorithmus ab,
00:56:52
aber eben auch von der Eingabe.
00:56:53
Also was für Daten gehen denn in den Algorithmus hinein?
00:56:57
Und da müssen wir unterscheiden, zum einen die Größe der Eingabe und dann natürlich die individuellen Werte.
00:57:03
Wie sieht die Eingabe aus? Und all das,
00:57:10
diese zwei Parameter hier, die sorgen für unterschiedliche physikalische Laufzeiten. Und trotzdem Die sind halt beide wichtig,
00:57:18
aber trotzdem werden wir die beide so in dieser Form nicht berücksichtigen können,
00:57:21
weil wenn wir die individuellen Werte berücksichtigen wollen,
00:57:24
dann können wir ja nicht sagen,
00:57:25
der Algorithmus hat irgendeine spezielle Qualität, dann würden wir sagen,
00:57:30
der Algorithmus hat bei der Eingabe die und die Laufzeit,
00:57:32
aber das bringt uns ja nicht weiter,
00:57:34
weil es gibt einfach in der Regel so viele verschiedene mögliche Eingabefolgen.
00:57:39
Also wenn wir zum Beispiel Zahlen sortieren,
00:57:40
das ist das Beispiel, wäre eben die Größe der Größenparameter,
00:57:44
wie viel Zahlen sollen dort sortiert werden und der zweite Parameter
00:57:47
bezüglich der individuellen Werte wäre,
00:57:50
in welcher initialen Reihenfolge liegen diese Zahlen denn vor.
00:57:54
Das hat sicherlich einen Einfluss,
00:57:56
also für viele Sortierverfahren hat das einen Einfluss auf die Laufzeit
00:58:02
Ja, dementsprechend muss man sich natürlich streng genommen damit auseinandersetzen.
00:58:07
Das machen wir auch, das machen wir dadurch,
00:58:10
dass wir für die verschiedenen Instanzen der gleichen Größe uns damit beschäftigen,
00:58:16
was der Worst Case ist, der Average Case und der Best Case.
00:58:19
Und genau das ist das, was wir als Worst Case Analyse bezeichnen.
00:58:23
Wir betrachten alle Eingaben einer festen Länge und von denen
00:58:26
betrachten wir dann die ungünstigste Art,
00:58:31
die individuellen Werte quasi in diese Eingabe zu verteilen.
00:58:34
Das ist die Worst Case Analyse eines Algorithmus.
00:58:37
Und der Average Case entsprechend der statistische Mittelwert
00:58:41
Über alle, der Mittelwert, über alle möglichen individuellen Verteilungen von Werten,
00:58:47
gebt uns den Average Case. Best Case gibt es auch,
00:58:51
aber den braucht man in der Regel so selten.
00:58:54
Dann werden wir auch kein einziges Mal sehen.
00:58:56
Das ist also einfach nur die Analyse im besten Fall.
00:58:59
Wir sehen hier fast immer Worst Case Analysen, ab und
00:59:02
zu Average Case Analysen. Das sind die beiden Fälle,
00:59:05
die wichtig sind. Die haben beide ihre Berechtigung,
00:59:09
also Worst Cases häufig in der Algorithmik wichtig,
00:59:13
weil sie Vorstellungen davon haben,
00:59:15
wie viel Zeit
00:59:16
ihr Algorithmus maximal benötigen darf
00:59:19
Ja, wenn sie eine iPhone-App schreiben, dann haben sie
00:59:22
eine Vorstellung davon, wie viele Millisekunden ihr Benutzer wartet,
00:59:26
bevor ihr lang ihr Tool doof findet.
00:59:28
Und dann muss die Worst-Case-Laufzeit ihres Algorithmus diese Laufzeitschranke einhalten.
00:59:34
Und dann nützt es auch nichts, dass der Mittelwert vielleicht
00:59:36
diese Laufzeitschranke einhält, weil wenn es eben Instanzen gibt,
00:59:40
wo es so lange dauert, ja, dann ist halt schlecht.
00:59:44
Und es gibt natürlich viele praktische Fälle, wo sie,
00:59:46
also gerade in Echtzeitsystemen, wo sie den Worst-Case genau verstehen müssen.
00:59:50
Ansonsten ist natürlich der Average-Case interessant, weil das ist halt das,
00:59:55
was im Mittel eintritt und es gibt ihnen natürlich ein gutes Gefühl über die Qualität des Algorithmus.
01:00:00
Häufig ist es so, selbst wenn die Worst-Case-Laufzeit von zwei Algorithmen gleich ist,
01:00:05
wenn der eine Algorithmus eine bessere Average-Case,
01:00:08
ein besseres Average-Case-Verhalten hat, ist es natürlich ein deutlicher Vorurteil.
01:00:14
Okay, da der Worst-Case der häufigste Fall in der Analyse ist,
01:00:17
ist es halt so, wenn wir nichts explizit sagen,
01:00:19
den meinen wir immer den Worst-Case.
01:00:23
Okay, O-Notationen kennen Sie hoffentlich sehr gut.
01:00:29
Also warum interessieren wir uns für die Laufzeit in der O-Notation?
01:00:34
Das liegt daran, weil wir uns das Wachstum von Funktionen anschauen.
01:00:39
Wir überlegen uns, wie verhält sich der Algorithmus mit immer größerem Input.
01:00:44
Und dann sehen wir, dass je nachdem, in welcher Funktionsklasse wir sind,
01:00:48
natürlich das Wachstumsverhalten der Zeit, des Funktionsparameters, extrem variiert.
01:00:54
Ja, wenn wir also eine Eingabe von 10.000 oder eine Million Datenelementen haben.
01:00:58
Und wir haben etwas, was einen linearen Zeitbedarf hat,
01:01:01
dann kostet das eben 10.000 oder eine Million Zeiteinheiten.
01:01:05
Wenn der Zeitbedarf quadratisch ist, kostet uns eben schon 100,
01:01:08
eine Million oder 10 hoch zwölf Zeiteinheiten.
01:01:13
Und genau dieses Wachstum ist für uns interessant zu verstehen,
01:01:17
wie verhält sich der Algorithmus für größere Eingaben, Egal,
01:01:23
welche Laufzeitklasse sie hier haben, für kleine Eingaben,
01:01:27
ist ihr Algorithmus in der Regel sowieso schnell.
01:01:30
Also wenn sie ein Grafproblem haben und ihre Eingabe hat sowieso
01:01:33
nur fünf oder zehn Knoten, dann ist es eigentlich fast egal,
01:01:37
was für eine Laufzeitklasse sie hier haben.
01:01:41
Ja, da spielen dann die Konstanten vielleicht schon eine wichtigere Rolle.
01:01:44
Aber wenn die Eingaben eben größer werden, dann werden die
01:01:46
Zeiten Laufzeit kritisch und dann spielt es eben eine große Rolle.
01:01:52
Ja, und gerade der Unterschied zwischen N-Log-An- und N-Quadrat hier,
01:01:57
ja, der sollte einem bewusst sein, weil so im Kopf,
01:02:01
im Bereich von Sortieren hat man das ja häufig.
01:02:03
Es gibt ein Quadratsortierverfahren in Log-in. Und dann denkt man so,
01:02:06
naja, ob End-Log-in oder in Quadrat, so what?
01:02:09
Aber wenn sie hier auf die Zahlen gucken,
01:02:11
dann sehen sie, dass es ein gravierender Unterschied ist.
01:02:14
Wenn sie hier in der Eingabegröße zwei Größenordnungen nach oben gehen,
01:02:19
dann haben sie eben einen Unterschied hier, der schon gravierend ist.
01:02:29
Also ein riesiger Laufzeitzuwachs, den sie einfach tolerieren müssen,
01:02:35
wenn sie wenn sie einen Quadratalgorithmus haben.
01:02:41
Und es gibt viele Probleme, wo die Ends so groß sind,
01:02:43
dass sich das Endquadrat schlicht und der Reifen nicht leisten können,
01:02:46
wo das Verfahren einfach zu langsam wird.
01:02:50
Okay, hier nochmal die Definition des Okalküls. Für die,
01:02:54
die es jetzt länger nicht mehr gesehen haben,
01:02:57
wir besagen eine Funktion F ist höchstens von der Ordnung gehe,
01:03:00
falls es konstant ein C und N-0 gibt mit null,
01:03:04
kleiner gleich F und N, kleiner gleich zehnmal G von N,
01:03:07
für alle N, die größer sind als diese konstante N-0.
01:03:13
Oder etwas kürzer aufgeschrieben,
01:03:14
es existiert eine konstante C größer Null und es existiert eine konstante 0 größer,
01:03:19
0, sodass für alle N größer als N0,
01:03:22
0, Kleiner gleich F von N,
01:03:23
Kleiner gleich 10 mal G von N gilt.
01:03:25
Dann schreiben wir, F&N ist gleich O von G von N.
01:03:31
Und damit ist gemeint, dass diese Funktion F&N bezüglich ihres
01:03:37
Wachstums in der Klasse der Funktion G von N ist.
01:03:40
In der gleichen Wachstumsklasse wie die Funktion G von N. So,
01:03:46
damit ist ja das O von G von N streng genommen eine Menge.
01:03:49
Das ist die Menge aller Funktionen, die genauso wachsen,
01:03:52
wie die Funktion G von N. Ja, so kann man es ja interpretieren.
01:03:56
Und trotzdem verwenden wir ein Gleichheitszeichen und kein Elementssymbol,
01:04:02
dass es in der Literatur nicht konsistent,
01:04:05
also gerade in mathematisch orientierten Büchern, sehen sie auch häufiger das Elementsymbol.
01:04:09
Wir verwenden hier das gleiche Zeichen,
01:04:10
der Com macht das auch und sie sollten es möglichst auftun
01:04:13
und ich werde ihnen gleich auch noch Gründe nennen,
01:04:15
warum wir das Gleichheitszeichen machen, weil wir nicht immer die Menge meinen.
01:04:21
Häufig meinen wir, wenn wir von O von G von
01:04:23
entsprechend eben deinen Repräsentanten daraus und dann ist das durchaus sinnvoll,
01:04:29
ein Gleichheitszeichen zu verwenden und deswegen verwenden wir konsistent Gleichheitszeichen.
01:04:35
Okay, neben dem Großohr gibt es das Kleino,
01:04:37
das Kleino beschreibt ein echt stärkeres oder schwächeres Wachstum,
01:04:41
je nach in welche Richtung sie gucken.
01:04:43
Da ist also das Kleinergleich hier. Er setzt durch einen Kleiner.
01:04:47
Dann gibt es das Omega für die unteren Schranken. Wenn man dann sagt,
01:04:49
F ist mindestens von Ordnung G und das Kleine Omega für eine echte untere Schranke,
01:04:56
ja, wenn man sagt,
01:04:57
das F von N ist echt größer als G von N.
01:05:00
Für alle möglichen konstanten C, die wir uns ausdenken können, ja.
01:05:05
Und das Täter, was quasi eine obere und untere Schranke,
01:05:08
also O und Omega, gleichzeitig bedeutet.
01:05:12
Rechtenregel fürs Okakül, kennen Sie hoffentlich auch alle.
01:05:16
Also jede Funktion ist natürlich von der Größenordnung der Funktion selber,
01:05:19
wenn Sie zwei Funktionen haben, die von der Orga gleichen Ordnung F ist,
01:05:23
dann ist das die Summe der Funktionen immer noch von der Ordnung F,
01:05:26
wenn sie eine Konstante drauf multiplizieren,
01:05:28
dann ändert es nichts von der bezüglich der Größenordnung,
01:05:31
ja, weil Konstanten ja sowieso frei wählbar sind im Okalkül.
01:05:36
Sie haben so eine Art Transitivitätsregel,
01:05:40
wenn F von der Größenordnung O von Groß-F ist und G
01:05:43
in der Größenordnung von O von Klein F,
01:05:46
dann müssen sie das G auch in der Größenordnung groß O von Groß-F ist.
01:05:51
Sie können Funktionen miteinander multiplizieren, dann müssen sie auch die Schranken,
01:05:55
die Funktionen innerhalb des Okalküls hier miteinander multiplizieren kann auch eine Funktion herausziehen.
01:06:02
Hier muss man allerdings teilweise ein bisschen aufpassen mit Vorzeichen und so.
01:06:05
Da darf natürlich nichts negativ sein, sonst funktioniert das nicht.
01:06:10
Und dementsprechend damit rechnen. All diese Regeln kann man beweisen, dass die gültig sind. Diese Beweise sind relativ einfach. In der Regel muss man nur die Definition anwenden,
01:06:21
ja, wie hier zum Beispiel für diese Regel 5 mit dem Produkt,
01:06:25
ja, dann wissen wir, haben wir die Definition für die,
01:06:30
wenn wir die Definition an für das F gleich O von F und dann,
01:06:34
die steht hier und für das G von gleich O von G,
01:06:38
die Definition und steht hier, dann haben wir entsprechende Konstanten,
01:06:41
N-0 und 10-0, sodass halt für alle N größer,
01:06:44
gleich ein Null,
01:06:45
er von den Kleidern gleich 10-0 malt F von N ist,
01:06:47
oder geh von in Kleiner gleich C-1 mal Großgeh von N,
01:06:51
naja, und dann können wir auch eine neue Funktion H definieren,
01:06:53
ist Produkt von den beiden, und dann gilt für alle N,
01:06:57
die größer sind als das Maximum von N-0 und N-1,
01:07:03
dass natürlich das Produkt dieser beiden Funktionen,
01:07:04
also H von in Kleiner gleich 10-0 mal F und N,
01:07:07
mal C-1 mal G von N ist,
01:07:09
und wir können die beiden Konstanten zusammenziehen,
01:07:11
und dann steht hier genau das, was wir eigentlich erwartet haben,
01:07:17
ja, so kann man all diese Rechenregeln,
01:07:18
die wir fürs O-Kalt-Tool kennen,
01:07:20
natürlich auch beweisen
01:07:23
Ja, Polynome sind im Okalkül immer vom Grad des höchsten Exponenten.
01:07:30
Ja, das ist der, der sozusagen die restlichen Therme dominiert. Die Konstanten spielen,
01:07:36
wie gesagt, keine Rolle, was manchmal irritierend sein kann,
01:07:39
weil Therme mit eigentlich niedrigerem Wachstum, aber sehr großen Konstanten,
01:07:45
im gesamten relevanten Bereich ihrer Eingabe die Laufzeit dominieren kann,
01:07:51
ja, und trotzdem natürlich im Okalkül unter den Tisch fallen.
01:07:53
Das ist übrigens einer der Schwachpunkte im Okalkül. Also es
01:07:57
gibt einfach Algorithmen, die im Okalkül schlechtere Laufzeitschranke haben,
01:08:02
in der Praxis aber eigentlich besser sind.
01:08:05
Weil für alle Eingabegrößen, die relevant sind, die konstanten kleiner sind.
01:08:11
Ja, bei Exponenten muss man ein bisschen aufpassen.
01:08:14
Die darf man natürlich nicht einfach einen Faktor weglassen,
01:08:16
wenn das im Exponenten vorkommt. Zwei Wochenende ist ein anderes
01:08:19
Wachstum als vier hoch N. Und bei Logorithmen,
01:08:23
da darf man hingegen ein bisschen schludern,
01:08:25
da darf man nämlich die Basis weglassen,
01:08:26
weil die eine Änderung der Basis wegen dem Basiswechselsatz nur eine weitere Konstante ist,
01:08:32
die wir dann vernachlässigen können.
01:08:37
Okay, so,
01:08:37
das ist sozusagen so ein bisschen Unnotation gewesen,
01:08:41
die Sie hoffentlich alle kennen
01:08:44
Und hier jetzt nochmal ein bisschen an der Argumentation für das Gleichheitszeichen.
01:08:55
Und ein Beispiel, wie wir mit dem O-Kalkül auch rechnen werden.
01:09:00
Und zwar lesen Sie manchmal sowas wie Zwei-End-Quadrat plus 3 in
01:09:05
plus 1, ist gleich 2 Endquadrat plus Täter von N.
01:09:10
Das ist eine wahre Aussage, so kann man das schreiben.
01:09:14
Und was damit gemeint ist, ist, glaube ich,
01:09:16
auch relativ schnell klar. Also hier hat jemand,
01:09:19
der das formuliert hat, der hat sich gedacht, ja,
01:09:22
okay, ich habe hier so ein mit dem Therm 2N-Quadrat,
01:09:24
das ist das, was also ein starkes Wachstum hat.
01:09:27
Und dann habe ich noch so Kleinkram, aber dieser Kleinkram,
01:09:29
der interessiert mich gar nicht so genau,
01:09:31
weil das Endquadrat hier hat das starke Wachstum,
01:09:33
das möchte ich einfach zusammenfassen und abschätzen.
01:09:36
Und dann sagt man,
01:09:37
okay, dass ihr das wächst halt so wie N,
01:09:40
also deswegen haben wir Tetter von N für diesen hinteren Teil und das ist ein Zwei-Endquadrat
01:09:44
Bus Tetter von N. Und jetzt stellt sich natürlich schon die Frage,
01:09:50
was das denn mathematisch jetzt hier bedeutet,
01:09:53
weil bis eben war das ja noch eine Menge.
01:09:55
Das war ja die Menge von allen Funktionen,
01:09:57
die so wachsen wie N. Und hier ist genau diese Stelle,
01:10:01
wo dem Tetter von N nicht die Menge,
01:10:03
sondern ein Repräsentant
01:10:03
gemeint ist
01:10:06
Was hier eigentlich steht in Kurzform ist, dass zwar Enquadrat
01:10:08
plus 3 und plus 1 das Gleiche ist wie 2N-Quadrat plus
01:10:12
F&N. Und FONN ist eine Funktion mit dem Wachstum Täter von N.
01:10:17
Einfach ein N ist gleich Täter von N. Das heißt,
01:10:20
was wir tun, ist, dass wir mit dem Täter
01:10:24
von N eigentlich einen Repräsentanten meinen, ohne ihn genau anzugeben.
01:10:28
Also wir sagen nicht, das ist genau diese Funktion,
01:10:30
sondern es ist irgendeine Funktion mit diesem Wachstum, also ein anonymer,
01:10:34
eine anonyme Funktion, von der wir nur das Wachstum kennen.
01:10:40
Frage? Das Gleiche, das hat ja nur,
01:10:43
was das gleiche Wachstum Genau, das ist nicht das Gleiche.
01:10:50
Also, also die Aussage hier ist die gleiche,
01:10:57
ja, die schon. Die Funktion Ephonin ist eben nur
01:11:00
ein Beispiel für eine Funktion mit linearem Wachstum und es könnte
01:11:02
die Funktion 3 in plus 1 sein.
01:11:04
Könnte auch eine andere sein, ja. Was man hier einfach nur sagt,
01:11:08
ist, dass wir hier einfach einen Therm haben,
01:11:12
der wächst linear und wir kümmern uns nicht um das Detail.
01:11:18
Darum geht es nicht
01:11:21
Gut, jetzt denkt man hier so, oh super,
01:11:24
also jetzt können wir mit dem Okalkül auch rechnen,
01:11:25
das ist ja klasse, dann könnten wir auch sowas schreiben,
01:11:28
wie O von N plus O von N-Of 3 oder irgendwie sowas,
01:11:31
könnten wir natürlich theoretisch auch tun.
01:11:34
Aber das eine, was man nicht tun darf, was absolut verboten ist,
01:11:38
ist eine O-Netation in parametrisierten Summen zu verwenden. Ja,
01:11:42
also wenn sie zum Beispiel sowas machen würden,
01:11:44
I gleich eins bis N-O von I,
01:11:47
ja, dann würden sie sagen,
01:11:48
aha, das ist ja sowas wie O von 1,
01:11:50
plus O von 2,
01:11:51
plus O von 3 und dann O von N-Minus 1
01:11:53
plus O von
01:11:55
Ja, und das ist hervorragend, weil dann wissen wir,
01:11:58
dass O von N ist ja der größte Therm hier,
01:12:00
das wächst ja am stärksten und dann können wir es
01:12:02
anderes weglassen und dann kommt da O von N raus.
01:12:05
Das ist natürlich falsch, weil wir wissen,
01:12:08
die Summe von I gleich 1 bis N der Zahlen I wächst quadratisch,
01:12:12
das kommt auch von ein Quadrat raus, also in parametrisierten Summen,
01:12:15
wenn da irgendwo Punkte oder sowas vorkommen, ober Summenzeichen,
01:12:18
dürfen sie niemals mit dem O-Kalkül arbeiten.
01:12:23
Ja,
01:12:23
erst nach Auflösen der Summe
01:12:27
So, und manchmal hat man dann die Situation,
01:12:30
dass das Okalkül auch auf beiden Seiten der Gleichung vorkommt.
01:12:33
Da würde man dann zum Beispiel im nächsten Schritt sagen,
01:12:35
zwei Endquadrat plus Tetter von N ist gleich Tetter von Endquadrat.
01:12:39
Und was ist jetzt gemeint? Ja,
01:12:42
jetzt ist es eben etwas anderes, ob wir das Tetter
01:12:45
auf der linken oder auf der rechten Seite betrachten.
01:12:47
Das Tetter auf der linken Seite, das kennen wir schon.
01:12:51
Das ist nämlich unsere anonyme Funktion, von der wir wissen,
01:12:53
ist irgendeine Funktion mit diesem linearen Wachstum.
01:12:57
Und das Tetter auf der rechten Seite ist jetzt aber die Klasse.
01:13:01
Also Tetter von N Quadrat, also so würde es
01:13:05
eben kennen
01:13:07
Okay, genau so ist es gemein. Und so werden wir
01:13:10
mit dem Okkakül dann auch entsprechend umgehen. Okay, so,
01:13:14
es gibt eine Reihe von Faktoren, die da natürlich eine Rolle spielen.
01:13:20
Es gibt konstante Faktoren, es gibt auch ein additiver Therm,
01:13:23
wenn sie so wollen, ja, der da draufkommen kann.
01:13:26
Und all die haben natürlich einen großen Einfluss darauf,
01:13:28
wie die reale Funktion aussieht. Ja,
01:13:31
und trotzdem ist es dann so,
01:13:33
dass es immer irgendwann diese konstante N0 gibt,
01:13:36
ab der dann die Funktion tatsächlich auch vom Wert her größer sein muss,
01:13:40
als die Funktion F&N.
01:13:42
Ja, also wenn
01:13:43
wir F&N und GVN haben
01:13:48
Gut, noch ganz kurz zur Laufzeitanalysen, wie wir die machen.
01:13:52
Die Operationen weisen wir auf Zeitkonstanten in der Regel zu,
01:13:56
die meisten Operatierungen kostenkonstante Zeit,
01:13:58
Schleifen haben die Anzahl der Schleifendurchläufe als wichtigste Parameter.
01:14:04
Funktionsaufrufe sind konstant und Rekussionen benötigen eben die Zeit der rekusiven Funktion.
01:14:10
Und hier jetzt noch das angegekündigte Beispiel für die Berechnung der Exponentialfunktion,
01:14:18
der andere Algorithmus, um das Ganze zu tun.
01:14:22
Ja, wenn wir den ersten nochmal, wenn Sie sich nochmal
01:14:24
den ersten Kopf überlegen, der hat ja Folgendes gemacht.
01:14:27
Der hat ja den Wert A einfach B oder hier ist
01:14:31
es jetzt K. Also wir wollen A auch K mal,
01:14:33
also K mal aufmultipliziert und das war dann das Ergebnis.
01:14:36
Das heißt, die Laufzeit unseres Algorithmus war linear in K
01:14:41
, wenn sie so wollen.
01:14:42
Also er war O von K, hatte der Algorithmus.
01:14:45
So, hier ist ein alternativer Algorithmus, der den Exponenten berechnet.
01:14:52
Und zwar geht der Algorithmus wie Volks vor.
01:14:55
Wir verwenden drei Variablen, PQ und L.
01:14:58
Am Anfang ist die Variable P1, die Variable Q A
01:15:02
und die Variable L kriegt den Wert
01:15:06
Und dann haben wir eine Wildschleife, solange dieses L
01:15:09
noch größer gleich 1 ist, machen wir folgendes.
01:15:12
Wenn L-Modulu 2 gleich 1 ist, das heißt,
01:15:17
wenn L eine ungerade Zahl ist, dann werden wir P mit Kuh multiplizieren.
01:15:22
Also das ist ungefähr das, was wir vorher auch gemacht haben.
01:15:25
Da hatten wir dann vorher, haben wir dann immer einmal das A drauf multipliziert.
01:15:30
Hier nehmen wir eine andere variable Kuh, was wird dir da drauf multipliziert?
01:15:35
Dann machen wir eine ganzzahlige Division durch 2 für das L,
01:15:38
also das DIF ist ganz zahlig.
01:15:40
Und dann quadrieren wir das Kuh. Okay, so,
01:15:47
das Ist unser Algorithmus, der läuft hier durch und irgendwann
01:15:51
haben wir das Ergebnis berechnet und das soll dann in P stehen.
01:15:55
Da stellt sich jetzt natürlich erstmal die Frage, wie lange dauert das?
01:15:59
Naja, eine Analyse im Okalkül von diesem sehr einfachen Verfahren würde dann ergeben.
01:16:03
Sie haben ganz viele Operationen, die konstante Zeit benötigen.
01:16:07
Dann haben Sie diese Wildschleife und hier müssen Sie sich überlegen,
01:16:09
wie viele Schleifendurchläufe macht diese Wildschleife. Und dazu müssen Sie
01:16:13
gucken, was mit den Parametern in der Wildschleife passiert.
01:16:17
Und Sie sehen, naja, das L hier,
01:16:18
das wird immer ganz zeitig durch zwei dividiert und dementsprechend können
01:16:23
wir das natürlich nur Logerithmus zu Basis 2 von K,
01:16:29
war Kaba der ursprüngliche Wert mal machen.
01:16:31
Und dann ist der Wert natürlich kleiner als eins geworden.
01:16:36
Und dementsprechend ist nach Logorithmus zu Weises 2 von Carplus 1
01:16:41
durchlaufen, der Wert L hier null geworden.
01:16:45
Und die Schleife wird abbrechen. Dann wissen wir, wie
01:16:47
viele Schleifendurchläufe wir haben. Und damit können wir die Laufzeit angeben.
01:16:51
Das wäre dann auch von locker. Der Algorithmus ist also
01:16:54
wesentlich effizienter als der, den wir gerade gesehen haben.
01:17:01
Speichert war, können Sie sich auch noch Gedanken darüber machen.
01:17:03
Das ist ja auch trivial. Sie haben ja nur
01:17:04
ein paar Konstanten, also ein paar Variablen,
01:17:06
eine konstante Anzahl
01:17:09
Das. Und die spannendere Frage bei diesem Algorithmus ist eigentlich,
01:17:12
warum ist der exakt, warum berechnet der überhaupt A auch K?
01:17:15
Ich weiß gar nicht, wie viele von ihnen kennen den Algorithmus?
01:17:17
Wer hat den schon mal gesehen? So ein paar,
01:17:23
ne? Also wieso berechnet der tatsächlich A hoch K?
01:17:28
Eine Frage? Wie kommen die auf einmal
01:17:31
auf die Lok von K und ich kam halt so?
01:17:34
Also für mich ist das in die K. Also der Wert K hier,
01:17:43
so ein ganz klein bisschen Tafel habe ich ja,
01:17:44
aber keine Kreide.
01:17:45
Das ist irgendwo
01:17:46
gerade wieder
01:17:47
Der wird K. hier, der halbiert sich in jedem Schleifendurchlauf.
01:17:52
Wenn der am Anfang, sagen wir mal, sieb...
01:17:55
Okay, gut. Okay, also warum ist
01:18:00
der Algorithmus exakt und wie kann man das zeigen?
01:18:03
Hier oben steht schon die Schleifen in Variante.
01:18:06
Und das ist für mich ein Paradebeispiel für einen Algorithmus mit einer
01:18:12
ganz einfachen Schleifen in Variante, die ganz schwer zu finden ist.
01:18:17
Also die Schleifen in Variante, die hier besagt,
01:18:20
dass A auch K, also das,
01:18:22
was wir eigentlich berechnen wollen,
01:18:23
zu jedem Zeitpunkt P mal Kuh hoch L ist
01:18:29
Und wir gucken mal, also am Anfang des Algorithmus ist ja
01:18:33
P hier 1 und Q ist A und L entspricht K.
01:18:36
Das heißt, hier steht einmal A hoch K.
01:18:39
Also es ist am Anfang auf alle Fälle mal korrekt.
01:18:42
Also nach der, vor dieser Wildschleife hier. Aber
01:18:45
jetzt wird es komisch, weil das L wird verändert,
01:18:48
das wird immer durch zwei dividiert.
01:18:49
Das Q wird quadriert und hier wird das P immer noch
01:18:52
irgendwie multipliziert mit dem Q und irgendwie wirkt sich das natürlich
01:18:55
auf dieses PQ und L in der Schleife auf, aus.
01:18:59
Und trotzdem soll zu jedem Zeitpunkt, also zu jedem,
01:19:02
nach jedem Schleifendurchlauf wieder A auch K gleich P
01:19:05
mal Kuch L gelten
01:19:10
Ja, wenn wir am Ende des Algorithmus angekommen sind,
01:19:12
dann sehen wir,
01:19:14
dass genau diese Schleifen in Variante uns tatsächlich zu dem wichtigen Ergebnis führt,
01:19:18
weil am Ende ist ja L.0 und wenn wir dann Kuh hoch Null haben,
01:19:24
ja, dann ist das eins und dann wäre das also P,
01:19:26
mal eins, dann können wir das auch weglassen und wenn diese Innenvariante gilt,
01:19:29
dann wäre P gleich A hoch K und wenn wir P ausgeben hier in Schritt 6,
01:19:34
dann hätten wir tatsächlich das korrekte Ergebnis berechnet.
01:19:37
Wir müssen also nur zeigen, dass in der,
01:19:40
beim Durchlauf dieser Wildschleife diese Schleifen in Variante
01:19:44
tatsächlich korrekt ist
01:19:47
Also, vor Beginn der Schleife wissen wir schon,
01:19:50
dass sie korrekt ist. Das haben wir gerade schon gesehen.
01:19:52
PS1, QSA, LSK, auch KS gleich Pema,
01:19:55
Kuch L. Nach jedem Schleifendurchlauf gilt dann folgendes. Also,
01:20:03
wir müssen jetzt die zwei Fälle unterscheiden. Also,
01:20:05
das L, das kann entweder gerade oder ungerade sein.
01:20:07
Das ist die Fallunterscheidung hier in dem IF, ja.
01:20:11
Wenn das L gerade ist, also L,
01:20:12
Modulo 2 wäre gleich null, dann passiert Folgendes.
01:20:19
Wir bezeichnen mal mit 11 Strich- und Kuhstrich die Werte,
01:20:22
die wir vor der Zeile 3 haben und dann mit Q&L, die Werte danach.
01:20:27
Also hier Zeile 3 ist dann hier am Anfang der Schleife und dann,
01:20:32
also hier, das, was hier gilt, nennen wir jetzt P-Strich-L-Strich.
01:20:37
Und was am Ende gilt, ist dann PL und Co. So,
01:20:41
und dann wissen wir, dass AOK ist gleich P,
01:20:45
mal Kuh-Strich-Hoch-L-Strich, weil das war die Schleifen im Variante.
01:20:49
Ja, und jetzt hat unser Algorithmus Kuh und L verändert.
01:20:53
Es hat nämlich das Kuh quadriert und das heißt,
01:20:55
sein neues Kuh ist Kuh-Strich zum Quadrat und es hat L halbiert.
01:21:01
Das heißt, unser neues L ist L-Strich halbe
01:21:04
Und das ist natürlich das Gleiche, wenn wir das quadrieren und das hier halbieren,
01:21:08
weil das L ja eine gerade Zahl ist und wir keinen Rest haben, ist das das Gleiche.
01:21:12
Das heißt, das ist wieder P-Mal-Kuh-Hoch-L. Wenn das L ungerade ist,
01:21:19
dann können wir das so nicht machen,
01:21:22
weil dann hier das L-Halbe natürlich einen Rest hatte, den müssen wir berücksichtigen.
01:21:28
Und dann können wir aber sagen, das ist AOK,
01:21:30
also Vorausführung, galt dann P-Strich, Maku-Strich-Hoch-L-Strich.
01:21:36
Und da können wir jetzt mal einen Kuhstrich rausziehen,
01:21:38
wir formen das jetzt einfach oben,
01:21:39
und dann haben wir P-Strich-Maku-Strich und dann ist, dass L ja wieder gerade,
01:21:44
dann hast du es nämlich L minus 1, das ist wieder gerade.
01:21:47
Und dann können wir wieder den gleichen Trick machen wie hier oben,
01:21:49
dann ist das eben Kuh-Strich-Quadrat, Hoch-L-Strich-minus 1 halbe. Ja? So,
01:21:57
und dann können wir gucken und sagen, naja,
01:21:58
das Kuh wird ja quadriert und das L wird ganz zahlig durch zwei devidiert,
01:22:03
das heißt Kuh-Strich-Quadrat, ist das neue Kuh und das L-Strich-minus 1 halbe,
01:22:07
ist das neue L, naja,
01:22:11
und das P wird ja mit dem Kuh multipliziert,
01:22:13
das heißt P-Strich mal Kuh-Strich ist das neue P,
01:22:16
also steht ja auch wieder P, mal Kuh,
01:22:17
Hochel.
01:22:19
Und daraus folgt die Korrektheit des Algorithmus. Das ist,
01:22:21
wie gesagt, ein Paradebeispiel für die Anwendung von Schleifen in Varianten,
01:22:26
ja, und Es ist schwer zu sehen, ja,
01:22:30
dass man, man kann natürlich, was meistens hilft,
01:22:33
ist, dass man rückwärts guckt.
01:22:34
Man überlegt sich quasi, was müsste denn gelten,
01:22:37
dass ich, damit ich weiß, dass mein Ergebnis korrekt ist.
01:22:41
Ja, man guckt also in dem Algorithmus eher von unten nach oben.
01:22:43
Also ich überlege mir hier, naja, ich müsste irgendwie,
01:22:46
das P müsste irgendwie das A auch K sein,
01:22:48
weil das wäre ja die Ausgabe.
01:22:50
Und dann überlegt man sich von da an, naja,
01:22:53
was gilt vielleicht am Anfang und versucht sich so eine Regel abzuleiten,
01:22:59
was sozusagen in dieser Schleife als Innenvariante funktionieren könnte.
01:23:04
Okay, gut,
01:23:05
das dazu
01:23:07
Ganz kurz noch, das muss ich, die rekursiven Funktionen machen wir durch Rekurrenzen.
01:23:13
Auch das haben sie im Grundstudium schon hoffentlich intensivst betrieben.
01:23:19
Wir beschreiben die Laufzeit dann eben durch die Funktion selber und sagen,
01:23:22
TVN ist dann 10.0,
01:23:23
wenn N gleich 1 ist oder T von N minus 1 plus C1,
01:23:27
wenn wir den rekursiven Aufruf starten oder wir haben sowas wie zweimal
01:23:31
Tee von N halbe plus C. Wir gehen hier immer davon aus,
01:23:37
dass das TVN nur für natürliche Zahlen definiert.
01:23:40
Es ist manchmal schwierig, weil in halbe könnt ihr dann ja eine,
01:23:43
könnt ihr dann ja eine rationale Zahl werden.
01:23:47
Allerdings haben wir dann eine Rundungsphänomene, die wir in den
01:23:49
meisten Fällen einfach mal ignorieren
01:23:53
Wir gehen eigentlich immer davon aus, dass die Laufzeit konstant ist für kleine N.
01:23:58
Und wie gesagt, dass die Rundung, die vernachlässigen wir,
01:24:00
weil die uns einfach sehr viel, ja,
01:24:03
die machen die Analyse sonst halt extrem komplex und meistens wirken sie sich auch nicht aus.
01:24:06
Sonst muss man natürlich natürlich genauer eingucken. Das Trickige hier
01:24:12
bei den rekursiven Funktionen ist, das Suchen der geschlossenen Formel für TVN.
01:24:18
Die Standardmethode ist erstmal eine Substitutionsmethode. Sie haben die Gleichung,
01:24:22
sie setzen das hier ein paar Mal ein.
01:24:24
Wenn sie sagen TVN-1 ist ja TVN-minus 2 plus C1 und
01:24:28
dann setzen wir das nochmal ein und nochmal und nochmal.
01:24:30
Und dann haben sie hier sowas wie T von N- minus 1 plus,
01:24:34
C1 plus 21 plus C1 und so weiter, das ganze N-minus 1 mal.
01:24:39
Und dann wissen sie, dass sie es T1 und dann
01:24:41
haben sie N-minus 1 mal diese Konstante und dann sehen sie das O von N.
01:24:45
Das ist die Substitutionsmethode, die geht immer,
01:24:47
wenn nicht ganz, ganz einfache Funktionen habe.
01:24:51
Auch bei dieser Art zweimal T von N halbe plus C-Funktion geht das noch relativ gut. Ja,
01:24:58
wenn sie das ein paar Mal einsetzen hier,
01:25:01
dann sehen sie am Ende,
01:25:02
kommt da sowas raus wie zwei hoch I mal Tee von N durch 2 Hoch I,
01:25:07
ja,
01:25:08
weil sie hier immer durch zwei dividieren und dann haben sie hier diese ganze Summe von diesen Thermen,
01:25:13
die alle verschiedene Zweierpotenzen haben,
01:25:15
also zwei UI minus 1 mal C plus 2 minus
01:25:17
2 mal C und so weiter
01:25:21
So, und dann, ja, überlegt man sich,
01:25:25
wie kann man das hier aufschreiben, durch eine Summenformel,
01:25:27
dann sähe das so aus,
01:25:28
dann hat man zwei auch ihm mal TON-Tee von N durch
01:25:32
2 hochi plus und dann die Summe von K gleich 0 bis i minus 1, 2 hoch
01:25:36
k mal C. Das ist sozusagen der intuitive Schritt,
01:25:41
wie sie quasi die Summenformel erstmal finden für die Rekurrenz.
01:25:46
Das Nächste ist, dass man sich überlegt,
01:25:48
wie viele Subtizitionsschritte, Substitutionsschritte notwendig sind und dann überlegen sich,
01:25:53
ja, wann wird das denn hier konstant?
01:25:55
Also das ist natürlich dann der Fall, wenn das N
01:25:57
durch 2 hochi kleiner gleich 1 wird Und das können Sie umformen.
01:26:01
Das ist dann der Fall, wenn das I größer gleich
01:26:04
Logorithmus zur Weise 2 von N wird. Und wenn Sie das dann rausgefunden haben,
01:26:09
können Sie das einsetzen, dann wissen Sie,
01:26:12
dass diese Summe hier immer kleiner, gleich zwei Hochlogrithmus zu beißt,
01:26:16
zwei von N, von T von 1 plus zehnmal,
01:26:19
K gleich null bis Logorithmus zur Weise,
01:26:21
zwei von N, zwei hoch K ist.
01:26:24
Hier seht ihr. Hier sehen Sie schon so ein Rundungsphänomen,
01:26:29
was hier jetzt nicht mehr berücksichtigt wurde.
01:26:33
Also normalerweise hätte man jetzt hier noch mit einem Login aufpassen müssen,
01:26:35
das müsste man aufrunden eigentlich,
01:26:38
damit das
01:26:38
ganz korrekt ist
01:26:40
Ja, und dann müssen sie diese Summe hier auflösen.
01:26:42
Das geht ganz einfach, weil das ist hier die geometrische
01:26:46
oder exponentielle Reihe. Dafür kennen wir eine geschlossene Summenformel.
01:26:51
Und dann steht da N mal C plus C,
01:26:54
mal zwei Hochlocke 2 N plus 1, minus 1.
01:26:56
Und das können sie auflösen. Und das ist dreimal zehnmal
01:26:59
in minus C, also O von N. Das ist die
01:27:03
Art und Weise, wie wir einfache rekusive Gleichungen auflösen können.
01:27:10
Das ist natürlich streng genommen nicht vollständig hier. Hier haben
01:27:12
wir es nur ausgerechnet. Wir müssen es noch beweisen,
01:27:15
dass das korrekt ist. Wenn man das dann macht,
01:27:18
dann macht man einen Induktionsbeweis. Und hier gibt es manchmal
01:27:24
Eine unangenehme Situation. Also wenn man das so ad hoc macht,
01:27:30
dann würde man wahrscheinlich wie folgt vorgehen und würde sagen,
01:27:33
ja, TVN ist ja kleiner gleich K mal N für irgendeine Konstante,
01:27:38
weil das soll ja hier linear sein.
01:27:41
Und dann setzen, sagen sie, das ist meine Annahme,
01:27:43
die wollen sie jetzt zeigen für alle N. Und dann sagen sie,
01:27:46
gilt das jetzt für N gleich 1, dann sagen sie,
01:27:48
ja, das gilt für N gleich 1, weil TVN 1 ist C.
01:27:51
Und ich muss nur eine konstante K wählen,
01:27:53
die größer gleich C ist und dann gilt das natürlich.
01:27:56
Und dann sagen sie prima,
01:27:57
jetzt muss ich ja nur noch einen Induktionsschritt machen und dann sage ich,
01:27:59
sehe ich aus,
01:28:00
Tee von N ist gleich 2,
01:28:01
mal Tee von N halbe
01:28:04
Und dann sagen sie, Tee von Enhalbe,
01:28:05
das können sie natürlich, die Induktionsannahme einsetzen,
01:28:09
wäre also sowas wie K mal in halbe.
01:28:14
Und dann hebt sich die zwei hier auch hervorragend auf.
01:28:17
Und dann steht da Karl mal N plus 10. Das ist
01:28:20
doof. Ja, weil ihre Annahme war ja eigentlich,
01:28:24
Tee von En sollte kleiner gleich K mal N sein.
01:28:27
Jetzt steht da aber Karl mal N plus C.
01:28:31
Das heißt, der Induktionsbeweis hat jetzt nicht funktioniert.
01:28:33
Ja, sie haben diese Schranke nicht gezeigt oder nicht zeigen können.
01:28:38
Und das Intuitive, was man als nächstes tut,
01:28:40
ist, dass man sagt, ja,
01:28:41
da war die wohl zu klein,
01:28:42
da muss ich die halt größer machen
01:28:44
Sie hier reinschreiben, okay, das ist irgendwie karbmal N
01:28:48
plus C oder irgendwie sowas oder plus K-Strich oder irgendwie,
01:28:52
und machen sie es noch größer.
01:28:54
Der Punkt ist nur, je größer sie ihre Annahme machen,
01:28:58
umso größer ist auch der Therm,
01:29:00
den sie im Luktionsschritt einsetzen und dann wird es immer noch nicht hinhauen.
01:29:04
Und der Trick ist, dass sie die Schranke kleiner machen müssen.
01:29:07
Das ist etwas, was eigentlich entgegen der Intuition ist,
01:29:10
weil man das Gefühl hat, die ist ja hier nicht groß genug gewesen.
01:29:14
Man muss die Schranke Kleider machen, damit das funktioniert.
01:29:16
Also mit der Annahme karma N-C funktioniert der Beweis,
01:29:22
da sieht man dann hier, TV1 ist C, TV1 gleich C.
01:29:26
Das geht natürlich, wenn das Karl Größer gleich zweimal C ist.
01:29:30
Und im Induktionsschritt haben wir TVN gleich zweimal Themen von N halbe plus C.
01:29:34
Und das wäre zweimal K von N halbe minus C.
01:29:38
Und das wäre dann wieder kn-c. Gut,
01:29:43
wir werden nicht so viele Induktionsbeweise machen. Wir werden,
01:29:45
wenn wir eine Rekurrenz auflösen, auf diese Art und Weise,
01:29:51
dann werden wir annehmen, dass die dann auch korrekt ist.
01:29:55
Der Vollständigkeit halber muss man eigentlich diesen Induktionsbeweis dann auch
01:30:00
noch führen
01:30:02
Okay, so, ich habe eigentlich noch zwei,
01:30:04
drei Folien zu Rekurrenzen,
01:30:05
aber die kann ich Ihnen auch noch am Mittwoch zeigen,
01:30:09
damit Sie noch eine Chance haben,
01:30:10
was zu essen und wir sehen uns,
01:30:12
wie gesagt,
01:30:12
am Mittwoch
01:30:13
dann wieder